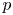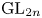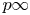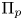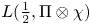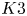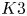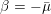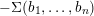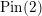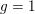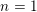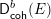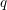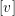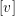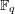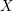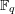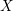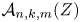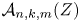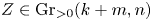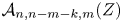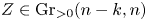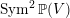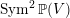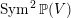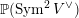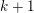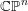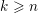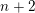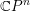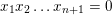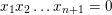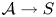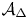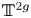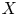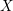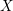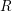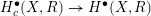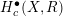Research Article
L-functions of GL2n: p-adic properties and non-vanishing of twists
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2437-2468
-
- Article
- Export citation
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2020, pp. 1965-2019
-
- Article
- Export citation
Pin(2)-equivariant Seiberg–Witten Floer homology of Seifert fibrations
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2019, pp. 199-250
-
- Article
- Export citation
Computing a categorical Gromov–Witten invariant
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1275-1309
-
- Article
- Export citation
Ordinary primes in Hilbert modular varieties
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2020, pp. 647-678
-
- Article
- Export citation
Higher-dimensional foliated Mori theory
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1-38
-
- Article
- Export citation
A Witt Nadel vanishing theorem for threefolds
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2020, pp. 435-475
-
- Article
- Export citation
Characteristic directions of two-dimensional biholomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2020, pp. 869-880
-
- Article
- Export citation
Arithmetic diagonal cycles on unitary Shimura varieties
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1745-1824
-
- Article
- Export citation
Cuspidal cohomology of stacks of shtukas
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1079-1151
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global geometry on moduli of local systems for surfaces with boundary
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1517-1559
-
- Article
- Export citation
Parity duality for the amplituhedron
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2020, pp. 2207-2262
-
- Article
- Export citation
The homological projective dual of
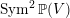 $\operatorname{Sym}^{2}\mathbb{P}(V)$
$\operatorname{Sym}^{2}\mathbb{P}(V)$
- Part of:
-
- Published online by Cambridge University Press:
- 17 January 2020, pp. 476-525
-
- Article
- Export citation
Rational cobordisms and integral homology
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2020, pp. 1825-1845
-
- Article
- Export citation
Homological mirror symmetry for higher-dimensional pairs of pants
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2020, pp. 1310-1347
-
- Article
- Export citation
The algebraic dimension of compact complex threefolds with vanishing second Betti number
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2020, pp. 679-696
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of algebraic solutions of irregular Garnier systems
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2020, pp. 881-907
-
- Article
- Export citation
Generic rank of Betti map and unlikely intersections
- Part of:
-
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2469-2509
-
- Article
- Export citation
Cohomology of generalized configuration spaces
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2019, pp. 251-298
-
- Article
- Export citation
On the Balmer spectrum for compact Lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2019, pp. 39-76
-
- Article
- Export citation