Article contents
Classification of algebraic solutions of irregular Garnier systems
Published online by Cambridge University Press: 14 April 2020
Abstract
We prove that algebraic solutions of Garnier systems in the irregular case are of two types. The classical ones come from isomonodromic deformations of linear equations with diagonal or dihedral differential Galois group; we give a complete list in the rank-2 case (two indeterminates). The pull-back ones come from deformations of coverings over a fixed degenerate hypergeometric equation; we provide a complete list when the differential Galois group is 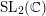 $\text{SL}_{2}(\mathbb{C})$. As a byproduct, we obtain a complete list of algebraic solutions for the rank-2 irregular Garnier systems.
$\text{SL}_{2}(\mathbb{C})$. As a byproduct, we obtain a complete list of algebraic solutions for the rank-2 irregular Garnier systems.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
Footnotes
We thank CNRS, Université de Rennes 1, Henri Lebesgue Center and ANR-16-CE40-0008 project ‘Foliage’ for financial support. We also thank the Simons Foundation’s project NLAGA which invited the two of us to Dakar, where we started working on this subject. We finally thank Hiroyuki Kawamuko and Yousuke Ohyama for helpful discussions on the subject.
References
- 2
- Cited by


