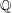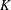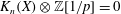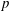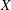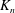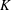Research Article
Modularity of nearly ordinary 2-adic residually dihedral Galois representations
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1235-1346
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum: Elliptic curves with a given number of points over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1347-1348
-
- Article
-
- You have access
- Export citation
Research Article
Fourier–Mukai functors in the supported case
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1349-1383
-
- Article
-
- You have access
- Export citation
Characterization of products of theta divisors
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1384-1412
-
- Article
-
- You have access
- Export citation
On the volume of isolated singularities
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2014, pp. 1413-1424
-
- Article
-
- You have access
- Export citation
Vanishing of negative
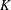 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1425-1434
-
- Article
-
- You have access
- Export citation
Metric Diophantine approximation on homogeneous varieties
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2014, pp. 1435-1456
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 150 Issue 8 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 150 Issue 8 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 August 2014, pp. b1-b3
-
- Article
-
- You have access
- Export citation