Article contents
Metric Diophantine approximation on homogeneous varieties
Published online by Cambridge University Press: 20 June 2014
Abstract
We develop the metric theory of Diophantine approximation on homogeneous varieties of semisimple algebraic groups and prove results analogous to the classical Khintchine and Jarník theorems. In full generality our results establish simultaneous Diophantine approximation with respect to several completions, and Diophantine approximation over general number fields using 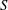 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$-algebraic integers. In several important examples, the metric results we obtain are optimal. The proof uses quantitative equidistribution properties of suitable averaging operators, which are derived from spectral bounds in automorphic representations.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$-algebraic integers. In several important examples, the metric results we obtain are optimal. The proof uses quantitative equidistribution properties of suitable averaging operators, which are derived from spectral bounds in automorphic representations.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 10
- Cited by


