Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-23T02:13:12.089Z Has data issue: false hasContentIssue false
  • English
  • Français

On the algebraic independence of generic Painlevé transcendents

Part of: Curves Model theory Differential equations in the complex domain

Published online by Cambridge University Press:  10 March 2014

Joel Nagloo  and
Anand Pillay
Joel Nagloo
Affiliation:
Department of Pure Mathematics, University of Leeds, UK email mmjcn@leeds.ac.uk
Anand Pillay
Affiliation:
Department of Mathematics, University of Notre Dame, IN 46556, USA email apillay@nd.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

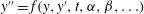We prove that if $y''=f(y,y',t,\alpha ,\beta ,\ldots)$ is a generic Painlevé equation from among the classes II, IV and V, and if 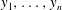$y_1,\ldots,y_n$ are distinct solutions, then 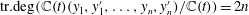$\mathrm{tr.deg}(\mathbb{C}(t)(y_1,y'_1,\ldots,y_n,y'_n)/\mathbb{C}(t))=2n$. (This was proved by Nishioka for the single equation 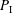$P_{{\rm I}}$.) For generic Painlevé III and VI, we have a slightly weaker result: 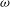$\omega $-categoricity (in the sense of model theory) of the solution space, as described below. The results confirm old beliefs about the Painlevé transcendents.

Keywords

Painlevé equationsalgebraic independencemodel theorydifferentially closed fields

MSC classification

Secondary: 14H05: Algebraic functions; function fields 14H70: Relationships with integrable systems 34M55: Painlevé and other special equations; classification, hierarchies; 03C60: Model-theoretic algebra
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 4 , April 2014 , pp. 668 - 678
Copyright
© The Author(s) 2014 

References

Boalch, P., The fifty-two icosahedral solutions to Painlevé VI, J. Reine Angew. Math. 596 (2006), 183–214.Google Scholar
Gromak, V., Laine, I. and Shimomura, S., Painlevé differential equations in the complex plane, De Gruyter Studies in Mathematics, vol. 28 (De Gruyter, 2002).Google Scholar
Kitaev, A., Law, C. and McLeod, J., Rational solutions of the fifth Painlevé equation, Differ. Integral Equations 7 (1994), 967–1000.Google Scholar
Lisovyy, O. and Tykhyy, Yu., Algebraic solutions of the sixth Painlevé equation, Preprint (2008), arXiv:0809.4873.Google Scholar
Marker, D., Model theory of differential fields, in Model theory of fields, Lecture Notes in Logic, vol. 5, eds Marker, D., Messmer, M. and Pillay, A. (Springer, Berlin–Tokyo, 2005).Google Scholar
Murata, Y., Rational solutions of the second and fourth Painlevé equations, Funkcial. Ekvac. 28 (1985), 1–32.Google Scholar
Murata, Y., Classical solutions of the third Painlevé equation, Nagoya Math. 139 (1995), 37–65.Google Scholar
Nagloo, R. and Pillay, A., On Algebraic relations between solutions of a generic Painlevé equation, Preprint (2011), arXiv:1112.2916.Google Scholar
Nishioka, K., Algebraic independence of Painlevé first transcendents, Funkcial. Ekvac. 47 (2004), 351–360.Google Scholar
Okamoto, K., Studies on the Painlevé equations IV, third Painlevé equation, P III, Funkcial. Ekvac. 30 (1987), 305–332.Google Scholar
Umemura, H. and Watanabe, H., Solutions of the second and fourth Painlevé equations, I, Nagoya Math. J 148 (1997), 151–198.Google Scholar
Watanabe, H., Birational canonical transformations and classical solutions of the sixth Painlevé equation, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) XXVII (1998), 379–425.Google Scholar