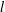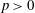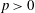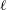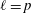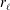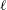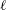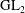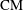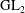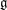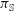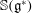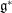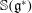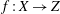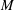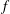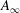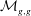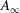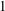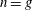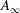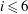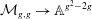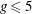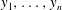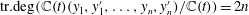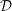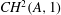Research Article
The
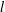 $l$-parity conjecture for abelian varieties over function fields of characteristic
$l$-parity conjecture for abelian varieties over function fields of characteristic 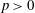 $p>0$
$p>0$
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 507-522
-
- Article
-
- You have access
- Export citation
Galois representations attached to automorphic forms on
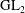 ${\rm GL}_2$ over
${\rm GL}_2$ over 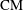 ${\rm CM}$ fields
${\rm CM}$ fields
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 523-567
-
- Article
-
- You have access
- Export citation
Deformations of the Lie–Poisson sphere of a compact semisimple Lie algebra
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 568-578
-
- Article
-
- You have access
- Export citation
Log canonical pairs with good augmented base loci
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 579-592
-
- Article
-
- You have access
- Export citation
Log pluricanonical representations and the abundance conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 593-620
-
- Article
-
- You have access
- Export citation
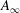 $A_{\infty }$-algebras associated with curves and rational functions on
$A_{\infty }$-algebras associated with curves and rational functions on 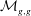 $\mathcal{M}_{g,g}$. I
$\mathcal{M}_{g,g}$. I
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 621-667
-
- Article
-
- You have access
- Export citation
On the algebraic independence of generic Painlevé transcendents
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 668-678
-
- Article
-
- You have access
- Export citation
The non-existence of stable Schottky forms
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 679-690
-
- Article
-
- You have access
- Export citation
Higher Chow cycles on Abelian surfaces and a non-Archimedean analogue of the Hodge-
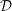 ${\mathcal{D}}$-conjecture
${\mathcal{D}}$-conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 691-711
-
- Article
-
- You have access
- Export citation
Abstract simplicity of locally compact Kac–Moody groups
- Part of:
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 713-728
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 150 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 May 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 150 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 May 2014, pp. f1-f4
-
- Article
-
- You have access
- Export citation