Article contents
Derived subalgebras of centralisers and finite 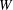 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
Published online by Cambridge University Press: 09 July 2014
Abstract
Let 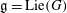 $\mathfrak{g}=\mbox{Lie}(G)$ be the Lie algebra of a simple algebraic group
$\mathfrak{g}=\mbox{Lie}(G)$ be the Lie algebra of a simple algebraic group 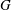 $G$ over an algebraically closed field of characteristic
$G$ over an algebraically closed field of characteristic 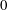 $0$. Let
$0$. Let  $e$ be a nilpotent element of
$e$ be a nilpotent element of 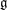 $\mathfrak{g}$ and let
$\mathfrak{g}$ and let 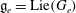 $\mathfrak{g}_e=\mbox{Lie}(G_e)$ where
$\mathfrak{g}_e=\mbox{Lie}(G_e)$ where 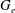 $G_e$ stands for the stabiliser of
$G_e$ stands for the stabiliser of  $e$ in
$e$ in  $G$. For
$G$. For 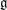 $\mathfrak{g}$ classical, we give an explicit combinatorial formula for the codimension of
$\mathfrak{g}$ classical, we give an explicit combinatorial formula for the codimension of 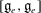 $[\mathfrak{g}_e,\mathfrak{g}_e]$ in
$[\mathfrak{g}_e,\mathfrak{g}_e]$ in 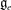 $\mathfrak{g}_e$ and use it to determine those
$\mathfrak{g}_e$ and use it to determine those 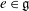 $e\in \mathfrak{g}$ for which the largest commutative quotient
$e\in \mathfrak{g}$ for which the largest commutative quotient 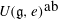 $U(\mathfrak{g},e)^{\mbox{ab}}$ of the finite
$U(\mathfrak{g},e)^{\mbox{ab}}$ of the finite 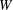 $W$-algebra
$W$-algebra 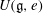 $U(\mathfrak{g},e)$ is isomorphic to a polynomial algebra. It turns out that this happens if and only if
$U(\mathfrak{g},e)$ is isomorphic to a polynomial algebra. It turns out that this happens if and only if  $e$ lies in a unique sheet of
$e$ lies in a unique sheet of 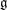 $\mathfrak{g}$. The nilpotent elements with this property are called non-singular in the paper. Confirming a recent conjecture of Izosimov, we prove that a nilpotent element
$\mathfrak{g}$. The nilpotent elements with this property are called non-singular in the paper. Confirming a recent conjecture of Izosimov, we prove that a nilpotent element 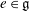 $e\in \mathfrak{g}$ is non-singular if and only if the maximal dimension of the geometric quotients
$e\in \mathfrak{g}$ is non-singular if and only if the maximal dimension of the geometric quotients 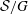 $\mathcal{S}/G$, where
$\mathcal{S}/G$, where 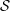 $\mathcal{S}$ is a sheet of
$\mathcal{S}$ is a sheet of 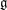 $\mathfrak{g}$ containing
$\mathfrak{g}$ containing  $e$, coincides with the codimension of
$e$, coincides with the codimension of 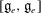 $[\mathfrak{g}_e,\mathfrak{g}_e]$ in
$[\mathfrak{g}_e,\mathfrak{g}_e]$ in 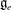 $\mathfrak{g}_e$ and describe all non-singular nilpotent elements in terms of partitions. We also show that for any nilpotent element
$\mathfrak{g}_e$ and describe all non-singular nilpotent elements in terms of partitions. We also show that for any nilpotent element  $e$ in a classical Lie algebra
$e$ in a classical Lie algebra 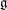 $\mathfrak{g}$ the closed subset of Specm
$\mathfrak{g}$ the closed subset of Specm 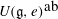 $U(\mathfrak{g},e)^{\mbox{ab}}$ consisting of all points fixed by the natural action of the component group of
$U(\mathfrak{g},e)^{\mbox{ab}}$ consisting of all points fixed by the natural action of the component group of 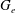 $G_e$ is isomorphic to an affine space. Analogues of these results for exceptional Lie algebras are also obtained and applications to the theory of primitive ideals are given.
$G_e$ is isomorphic to an affine space. Analogues of these results for exceptional Lie algebras are also obtained and applications to the theory of primitive ideals are given.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 15
- Cited by




