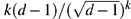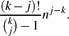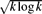Paper
Ewens Sampling and Invariable Generation
-
- Published online by Cambridge University Press:
- 12 April 2018, pp. 853-891
-
- Article
- Export citation
Christoffel–Darboux Type Identities for the Independence Polynomial
-
- Published online by Cambridge University Press:
- 02 April 2018, pp. 716-724
-
- Article
- Export citation
Correlation Bounds for Distant Parts of Factor of IID Processes
-
- Published online by Cambridge University Press:
- 01 August 2017, pp. 1-20
-
- Article
- Export citation
Triangle-Free Subgraphs of Random Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 141-161
-
- Article
- Export citation
Introduction
Introduction
-
- Published online by Cambridge University Press:
- 20 June 2018, p. 441
-
- Article
- Export citation
Paper
Ramsey Goodness of Bounded Degree Trees
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2018, pp. 289-309
-
- Article
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation
A (5,5)-Colouring of Kn with Few Colours
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2018, pp. 892-912
-
- Article
- Export citation
A Stronger Bound for the Strong Chromatic Index
-
- Published online by Cambridge University Press:
- 19 July 2017, pp. 21-43
-
- Article
- Export citation
Super-Exponential Extinction Time of the Contact Process on Random Geometric Graphs
-
- Published online by Cambridge University Press:
- 01 August 2017, pp. 162-185
-
- Article
- Export citation
Uniformly Discrete Forests with Poor Visibility
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2017, pp. 442-448
-
- Article
-
- You have access
- Export citation
Packing Graphs of Bounded Codegree
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2018, pp. 725-740
-
- Article
-
- You have access
- Open access
- Export citation
Triangle-Tilings in Graphs Without Large Independent Sets
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2018, pp. 449-474
-
- Article
- Export citation
New Classes of Degree Sequences with Fast Mixing Swap Markov Chain Sampling
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 186-207
-
- Article
- Export citation
Bisections of Graphs Without Short Cycles
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 44-59
-
- Article
- Export citation
Largest Components in Random Hypergraphs
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 741-762
-
- Article
- Export citation
On Quantitative Noise Stability and Influences for Discrete and Continuous Models
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2018, pp. 334-357
-
- Article
- Export citation
A Tutte Polynomial for Maps
-
- Published online by Cambridge University Press:
- 12 April 2018, pp. 913-945
-
- Article
- Export citation
The Growth Constant of Odd Cutsets in High Dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 208-227
-
- Article
- Export citation
Counting Intersecting and Pairs of Cross-Intersecting Families
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2017, pp. 60-68
-
- Article
- Export citation