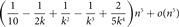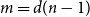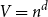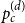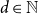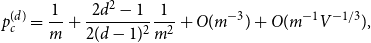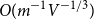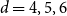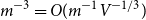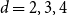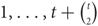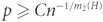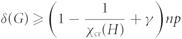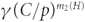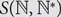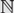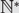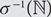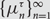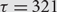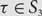Paper
On the Chromatic Number of Matching Kneser Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2019, pp. 1-21
-
- Article
- Export citation
Long Monotone Trails in Random Edge-Labellings of Random Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2019, pp. 22-30
-
- Article
- Export citation
On sets of points with few odd secants
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2019, pp. 31-43
-
- Article
- Export citation
Minimizing the number of 5-cycles in graphs with given edge-density
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2019, pp. 44-67
-
- Article
- Export citation
Expansion of Percolation Critical Points for Hamming Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2019, pp. 68-100
-
- Article
- Export citation
On Ramsey numbers of hedgehogs
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2019, pp. 101-112
-
- Article
- Export citation
On Komlós’ tiling theorem in random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 25 July 2019, pp. 113-127
-
- Article
- Export citation
Extensions of the Erdős–Gallai theorem and Luo’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2019, pp. 128-136
-
- Article
- Export citation
The Infinite limit of random permutations avoiding patterns of length three
- Part of:
-
- Published online by Cambridge University Press:
- 14 October 2019, pp. 137-152
-
- Article
- Export citation
The Induced Removal Lemma in Sparse Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2019, pp. 153-162
-
- Article
- Export citation