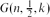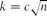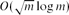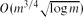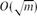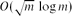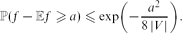Paper
Semi-Strong Colouring of Intersecting Hypergraphs
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 1-7
-
- Article
- Export citation
Short Proofs of Some Extremal Results
-
- Published online by Cambridge University Press:
- 04 November 2013, pp. 8-28
-
- Article
- Export citation
Finding Hidden Cliques in Linear Time with High Probability
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 29-49
-
- Article
- Export citation
Almost Every Tree With m Edges Decomposes K2m,2m
-
- Published online by Cambridge University Press:
- 03 December 2013, pp. 50-65
-
- Article
- Export citation
Applications of a New Separator Theorem for String Graphs
-
- Published online by Cambridge University Press:
- 25 October 2013, pp. 66-74
-
- Article
- Export citation
Component Games on Regular Graphs
-
- Published online by Cambridge University Press:
- 04 November 2013, pp. 75-89
-
- Article
- Export citation
The Distance-t Chromatic Index of Graphs
-
- Published online by Cambridge University Press:
- 14 November 2013, pp. 90-101
-
- Article
- Export citation
A Canonical Ramsey Theorem for Exactly m-Coloured Complete Subgraphs
-
- Published online by Cambridge University Press:
- 18 October 2013, pp. 102-115
-
- Article
- Export citation
A Marstrand Theorem for Subsets of Integers
-
- Published online by Cambridge University Press:
- 25 October 2013, pp. 116-134
-
- Article
- Export citation
Near-Optimal Separators in String Graphs
-
- Published online by Cambridge University Press:
- 07 October 2013, pp. 135-139
-
- Article
- Export citation
Concentration of Lipschitz Functionals of Determinantal and Other Strong Rayleigh Measures
-
- Published online by Cambridge University Press:
- 19 September 2013, pp. 140-160
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 23 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 December 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 23 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 December 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation