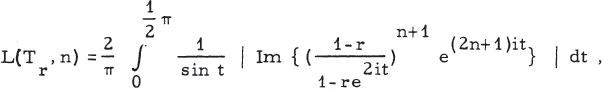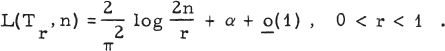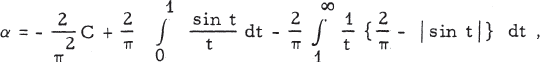Research Article
The Non-Biplanar Character of the Complete 9-Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-330
-
- Article
-
- You have access
- Export citation
A Characterization of Block-Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-6
-
- Article
-
- You have access
- Export citation
Notes on Number Theory III
On the Sum of Consecutive Primes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-161
-
- Article
-
- You have access
- Export citation
Research Article
Another Remark on a Result of K. Goldberg
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 7-9
-
- Article
-
- You have access
- Export citation
Small Positive Values of Indefinite Quadratic Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-339
-
- Article
-
- You have access
- Export citation
On the Multiplicity of Representations of Numbers by Sums
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 163-166
-
- Article
-
- You have access
- Export citation
The Hamilton-Jacobi Equations for a Relativistic Charged Particle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 341-350
-
- Article
-
- You have access
- Export citation
Notes on Number Theory V
Insolvability of
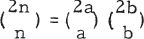
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-169
-
- Article
-
- You have access
- Export citation
Research Article
A Remark on a Result of Marvin Marcus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-13
-
- Article
-
- You have access
- Export citation
Asymptotic Variational Formulae for Eigenvalues
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 15-25
-
- Article
-
- You have access
- Export citation
The Hamilton-Jacobi Equation for a Charged Particle in a Combined Gravitational and Electromagnetic Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 351-358
-
- Article
-
- You have access
- Export citation
A Remark on Completely Monotonic Sequences, with an Application to Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 171-173
-
- Article
-
- You have access
- Export citation
Triangular Dissections of N-Gons
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-178
-
- Article
-
- You have access
- Export citation
A General Turán Expression for the Zeta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-366
-
- Article
-
- You have access
- Export citation
On Ordered Geometries
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-36
-
- Article
-
- You have access
- Export citation
Order in Affine and Projective Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 37-43
-
- Article
-
- You have access
- Export citation
On a Paper by M. Iosifescu and S. Marcus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 367-371
-
- Article
-
- You have access
- Export citation
The Lebesgue Constants for (γ, r) Summation of Fourier Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 179-182
-
- Article
-
- You have access
- Export citation
Some Results Concerning the Structure of Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 183-210
-
- Article
-
- You have access
- Export citation
Sur la Structure de Deux Classes D'anneaux
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-383
-
- Article
-
- You have access
- Export citation


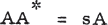
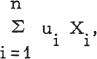 where u
where u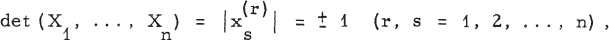


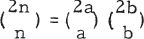


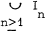
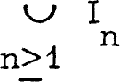 at 1 is zero. Let J
at 1 is zero. Let J