No CrossRef data available.
Article contents
A General Turán Expression for the Zeta Function
Published online by Cambridge University Press: 20 November 2018
Extract
In 1948 Gabor Szegő [9] gave four proofs of a remarkable inequality communicated to him by Paul Turán, who later published an original proof [10]. The Turán theorem states that if Pn(x) is the Le gendre polynomial, then
1.1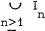
with equality holding only when |x| = 1.
Since then many similar inequalities have been found for various special functions, particularly for the Legendre and Hermite polynomials. Reference may be had to the recent work of Danese [2] and Chatterjea [1]. Danese gives an extensive bibliography.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1963


