Research Article
The Non-Biplanar Character of the Complete 9-Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-330
-
- Article
-
- You have access
- Export citation
Small Positive Values of Indefinite Quadratic Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-339
-
- Article
-
- You have access
- Export citation
The Hamilton-Jacobi Equations for a Relativistic Charged Particle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 341-350
-
- Article
-
- You have access
- Export citation
The Hamilton-Jacobi Equation for a Charged Particle in a Combined Gravitational and Electromagnetic Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 351-358
-
- Article
-
- You have access
- Export citation
A General Turán Expression for the Zeta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-366
-
- Article
-
- You have access
- Export citation
On a Paper by M. Iosifescu and S. Marcus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 367-371
-
- Article
-
- You have access
- Export citation
Sur la Structure de Deux Classes D'anneaux
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-383
-
- Article
-
- You have access
- Export citation
On the Reduction of Permutation Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-395
-
- Article
-
- You have access
- Export citation
Composition Theorems on Dirichlet Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 397-403
-
- Article
-
- You have access
- Export citation
On a Factorisation of Positive Definite Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 405-407
-
- Article
-
- You have access
- Export citation
A Property of Plane Sets of Constant Width
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 409-415
-
- Article
-
- You have access
- Export citation



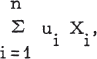 where u
where u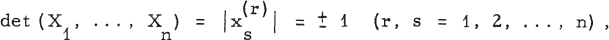
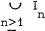
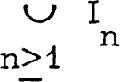 at 1 is zero. Let J
at 1 is zero. Let J