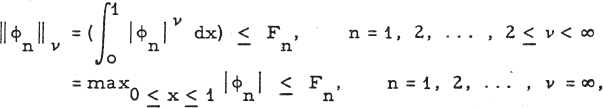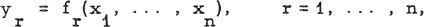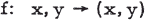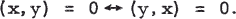Research Article
Remarks on an Arithmetic Derivative
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-122
-
- Article
-
- You have access
- Export citation
Some Extensions of the Hausdorff-Young and Paley Theorems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-138
-
- Article
-
- You have access
- Export citation
L'Esperance Mathematique du Nombre de Nombres Premiers Aleatoires Inferieurs ou Egaux A x
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-142
-
- Article
-
- You have access
- Export citation
On the Problem of Steiner
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 143-148
-
- Article
-
- You have access
- Export citation
Those Stirling Numbers Again
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-151
-
- Article
-
- You have access
- Export citation
A Finite Packing Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 153-155
-
- Article
-
- You have access
- Export citation
On the Colourings of Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-160
-
- Article
-
- You have access
- Export citation
The Reversibility of a Differentiable Mapping
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-181
-
- Article
-
- You have access
- Export citation
Right and Left Orthogonality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-184
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
Properties of Matter, by F.C. Champion and N. Davy. Third edition, Philosophical Library, New York, 1959. xvi + 334 pages. $10.00.
-
- Published online by Cambridge University Press:
- 01 April 2019, p. 199
-
- Article
-
- You have access
- Export citation
Proceeding of the International Congress of Mathematicians 1958, edited by J. A. Todd, E R. S. Cambridge University Press, Macmillan Company of Canada, 1960. lxiv + 573 pages. $11. 25.
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 197-198
-
- Article
-
- You have access
- Export citation
Reports Informations
Random Notes From the Secretariat
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 213-217
-
- Article
-
- You have access
- Export citation
Other
Solutions
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 187-194
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
Testing Statistical Hypotheses, by E. L. Lehmann. Wiley, New York, 1959. xiii + 369 pages. $11.00.
-
- Published online by Cambridge University Press:
- 01 April 2019, p. 198
-
- Article
-
- You have access
- Export citation
Grundlagen der Analysis, by Edmund Landau. Chelsea, New York, 1960. 173 pages. $1.95.
-
- Published online by Cambridge University Press:
- 01 April 2019, p. 208
-
- Article
-
- You have access
- Export citation
Other
News From the Departments
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 218-220
-
- Article
-
- You have access
- Export citation
Preliminary Report
Density Matrices of n-Fermion Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-212
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
Eléments d'histoire des mathématiques, by N. Bourbaki. Collection "Histoire de la pensée - IV" Hermann, Paris 1960. 276 pages. 18 NF.
-
- Published online by Cambridge University Press:
- 01 April 2019, pp. 199-202
-
- Article
-
- You have access
- Export citation
Research Article
On a Problem in Geometrical Probability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-186
-
- Article
-
- You have access
- Export citation
Book Reviews: Comptes Rendus Critiques
The Extension of Darboux's Method, by D. H. Parsons. Mémorial des Sciences mathématiques 14Z, Gauthier Villars, Paris, 1960. 75 pages. $4. 25 or 20 NF.
-
- Published online by Cambridge University Press:
- 01 April 2019, p. 207
-
- Article
-
- You have access
- Export citation