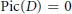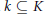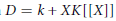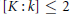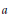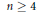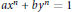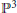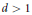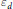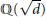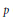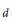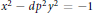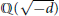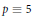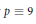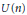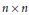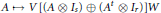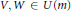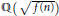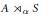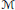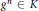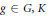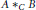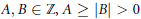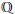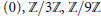Research Article
Condensed Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-13
-
- Article
-
- You have access
- Export citation
Generalized Commutativity in Group Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 14-25
-
- Article
-
- You have access
- Export citation
Remarques sur les points rationnels des variétés de Fermat
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-38
-
- Article
-
- You have access
- Export citation
Power Residue Criteria for Quadratic Units and the Negative Pell Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-53
-
- Article
-
- You have access
- Export citation
Linear Maps Transforming the Unitary Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-58
-
- Article
-
- You have access
- Export citation
A Note on Noncommutative Interpolation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 59-70
-
- Article
-
- You have access
- Export citation
The Number of Fields Generated by the Square Root of Values of a Given Polynomial
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 71-79
-
- Article
-
- You have access
- Export citation
Multi-Sided Braid Type Subfactors, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-94
-
- Article
-
- You have access
- Export citation
Cercles de remplissage for the Riemann Zeta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-97
-
- Article
-
- You have access
- Export citation
Crossed Products by Semigroups of Endomorphisms and Groups of Partial Automorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-112
-
- Article
-
- You have access
- Export citation
Properties of the
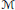 $\mathcal{M}$-Harmonic Conjugate Operator
$\mathcal{M}$-Harmonic Conjugate Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-121
-
- Article
-
- You have access
- Export citation
On Certain Finitely Generated Subgroups of Groups Which Split
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-129
-
- Article
-
- You have access
- Export citation
On Frankel’s Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-139
-
- Article
-
- You have access
- Export citation
An Explicit Cell Decomposition of the Wonderful Compactification of a Semisimple Algebraic Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-148
-
- Article
-
- You have access
- Export citation
The Ramification Polygon for Curves over a Finite Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-156
-
- Article
-
- You have access
- Export citation
Torsion Points on Certain Families of Elliptic Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-160
-
- Article
-
- You have access
- Export citation