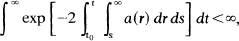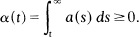Research Article
Finite Complexes and Integral Representations II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-9
-
- Article
-
- You have access
- Export citation
Lie Ideals in Associative Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 10-15
-
- Article
-
- You have access
- Export citation
Absolute Summability Factors in a Sequence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-30
-
- Article
-
- You have access
- Export citation
Additive Functionals on Lorentz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-37
-
- Article
-
- You have access
- Export citation
Primary Groups Whose Basic Subgroup Decompositions can be Lifted
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-42
-
- Article
-
- You have access
- Export citation
Split Graphs with Specified Dilworth Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-47
-
- Article
-
- You have access
- Export citation
Characterizations of *-Multiplication Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 48-52
-
- Article
-
- You have access
- Export citation
(HM)-Spaces and Measurable Cardinals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 53-57
-
- Article
-
- You have access
- Export citation
On Subspaces of Replete and Measure Replete Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 58-64
-
- Article
-
- You have access
- Export citation
Regular and Mercerian Generalized Lototsky Method
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-71
-
- Article
-
- You have access
- Export citation
Free Actions By Elementary Abelian 2-Groups on Stiefel Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 72-77
-
- Article
-
- You have access
- Export citation
On Evaluation Subgroups of Generalized Homotopy Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 78-86
-
- Article
-
- You have access
- Export citation
Simplicite des Groupes Unitaires Definis par un Facteur Simple
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-95
-
- Article
-
- You have access
- Export citation
Nearly Open, According to a Subset, Linear Maps Which are Open
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 96-101
-
- Article
-
- You have access
- Export citation
A Second Order Superlinear Oscillation Criterion
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 102-112
-
- Article
-
- You have access
- Export citation
The Fixed Subring of Some Groups of Ring Automorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-116
-
- Article
-
- You have access
- Export citation
An Improved Wintner Oscillation Criterion for Second Order Linear Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-121
-
- Article
-
- You have access
- Export citation
Centralizing Mappings of Prime Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-126
-
- Article
-
- You have access
- Export citation
Non-Parallelizability of Grassmann Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 127-128
-
- Article
-
- You have access
- Export citation

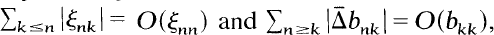 , where (ξ
, where (ξ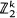 . We show that if
. We show that if 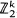 acts freely on
acts freely on 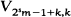 and
and
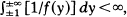 and
and 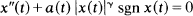 (γ > 1) this criterion leads to an oscillation result due to Wong [9].
(γ > 1) this criterion leads to an oscillation result due to Wong [9].