Article contents
Transcendental Solutions of a Class of Minimal Functional Equations
Published online by Cambridge University Press: 20 November 2018
Abstract
We prove a result concerning power series 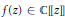 $f\left( Z \right)\,\in \,\mathbb{C}\left[\!\left[ Z \right]\!\right]$ satisfying a functional equation of
the form?
$f\left( Z \right)\,\in \,\mathbb{C}\left[\!\left[ Z \right]\!\right]$ satisfying a functional equation of
the form?
1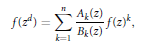 $$f\left( {{Z}^{d}} \right)\,=\,\sum\limits_{k=1}^{n}{\frac{{{A}_{k}}\left( Z \right)}{{{B}_{k}}\left( Z \right)}\,f{{\left( Z \right)}^{k}}},$$
$$f\left( {{Z}^{d}} \right)\,=\,\sum\limits_{k=1}^{n}{\frac{{{A}_{k}}\left( Z \right)}{{{B}_{k}}\left( Z \right)}\,f{{\left( Z \right)}^{k}}},$$
where 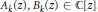 ${{A}_{k}}\left( Z \right),\,{{B}_{k}}\left( Z \right)\,\in \,\mathbb{C}\left[ Z \right]$. In particular, we show that if
${{A}_{k}}\left( Z \right),\,{{B}_{k}}\left( Z \right)\,\in \,\mathbb{C}\left[ Z \right]$. In particular, we show that if 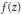 $f\left( Z \right)$ satisfies a minimal functional equation of the above form with
$f\left( Z \right)$ satisfies a minimal functional equation of the above form with 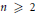 $n\,\ge \,2$, then
$n\,\ge \,2$, then 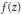 $f\left( Z \right)$ is necessarily transcendental. Towards a more complete classification, the case
$f\left( Z \right)$ is necessarily transcendental. Towards a more complete classification, the case 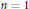 $n=\,1$ is also considered.
$n=\,1$ is also considered.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 1
- Cited by




