Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dai, Xinxin
2019.
Non-existence of $$*$$-Ricci solitons on $$(\kappa ,\mu )$$-almost cosymplectic manifolds.
Journal of Geometry,
Vol. 110,
Issue. 2,
Mallesha Naik, Devaraja
Venkatesha, V.
and
Aruna Kumara, H.
2020.
Ricci Solitons and Certain Related Metrics on Almost Co-Kaehler Manifolds.
Zurnal matematiceskoj fiziki, analiza, geometrii,
Vol. 16,
Issue. 4,
p.
402.
De, Uday Chand
Chaubey, Sudhakar K.
and
Suh, Young Jin
2020.
A note on almost co-Kähler manifolds.
International Journal of Geometric Methods in Modern Physics,
Vol. 17,
Issue. 10,
p.
2050153.
Chen, Xiaomin
and
De, Uday Chand
2021.
The k-almost Yamabe solitons and almost coKähler manifolds.
International Journal of Geometric Methods in Modern Physics,
Vol. 18,
Issue. 11,
p.
2150179.
Sardar, Arpan
Khan, Mohammad Nazrul Islam
and
De, Uday Chand
2021.
η-∗-Ricci Solitons and Almost co-Kähler Manifolds.
Mathematics,
Vol. 9,
Issue. 24,
p.
3200.
Chen, Xiaomin
2021.
Cotton solitons on almost cokähler 3-manifolds.
Quaestiones Mathematicae,
Vol. 44,
Issue. 8,
p.
1055.
De, Uday Chand
Suh, Young Jin
and
Chaubey, Sudhakar K.
2021.
Conformal vector fields on almost co-Kähler manifolds.
Mathematica Slovaca,
Vol. 71,
Issue. 6,
p.
1545.
Sarkar, Avijit
Halder, Suparna
and
De, Uday
2022.
Riemann and Ricci bourguignon solitons on three-dimensional quasi-Sasakian manifolds.
Filomat,
Vol. 36,
Issue. 19,
p.
6573.
Suh, Young Jin
2022.
Fischer–Marsden conjecture on real hypersurfaces in the complex hyperbolic two-plane Grassmannians.
Analysis and Mathematical Physics,
Vol. 12,
Issue. 5,
Li, Jin
and
Liu, Ximin
2022.
Ricci Solitons on Homogeneous Almost $$\alpha $$-Cosymplectic Three-Manifolds.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 1,
Chaubey, Sudhakar K.
and
Vîlcu, Gabriel-Eduard
2022.
Gradient Ricci solitons and Fischer–Marsden equation on cosymplectic manifolds.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 4,
Wang, Wenjie
2022.
Almost Cosymplectic $$(k,\mu )$$-metrics as $$\eta$$-Ricci Solitons.
Journal of Nonlinear Mathematical Physics,
Vol. 29,
Issue. 1,
p.
58.
Biswas, Gour
Chen, Xiaomin
and
De, Uday
2022.
Riemann solitons on almost co-Kähler manifolds.
Filomat,
Vol. 36,
Issue. 4,
p.
1403.
Sardar, Arpan
and
Sarkar, Avijit
2022.
Ricci–Yamabe solitons on a class of generalized Sasakian space forms.
Asian-European Journal of Mathematics,
Vol. 15,
Issue. 09,
De, Uday Chand
Khan, Mohammad Nazrul Islam
and
Sardar, Arpan
2022.
h-Almost Ricci–Yamabe Solitons in Paracontact Geometry.
Mathematics,
Vol. 10,
Issue. 18,
p.
3388.
Wang, Wenjie
2022.
K-cosymplectic metric as an η-Ricci soliton.
International Journal of Geometric Methods in Modern Physics,
Vol. 19,
Issue. 05,
Rashmi, S.V. Divya
and
Venkatesha, V.
2022.
Almost *-η-Ricci solitons on Kenmotsu pseudo-Riemannian manifolds.
Analysis,
Vol. 42,
Issue. 4,
p.
241.
Suh, Young Jin
2023.
Fischer-Marsden conjecture on real hypersurfaces in the complex quadric.
Journal de Mathématiques Pures et Appliquées,
Vol. 177,
Issue. ,
p.
129.
Biswas, Gour Gopal
and
De, Uday Chand
2023.
Gradient ρ-Einstein solitons on almost Co-Kähler manifolds.
International Journal of Geometric Methods in Modern Physics,
Vol. 20,
Issue. 06,
Sardar, Arpan
De, Uday
and
Suh, Young
2023.
Conformal vector fields on f-cosymplectic manifolds.
Filomat,
Vol. 37,
Issue. 17,
p.
5649.
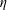 $\unicode[STIX]{x1D702}$-Einstein condition with constant coefficients is a Ricci soliton with potential vector field being of constant length, then either the manifold is Einstein or the Reeb vector field is parallel. Let
$\unicode[STIX]{x1D702}$-Einstein condition with constant coefficients is a Ricci soliton with potential vector field being of constant length, then either the manifold is Einstein or the Reeb vector field is parallel. Let 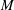 $M$ be a non-co-Kähler almost co-Kähler 3-manifold such that the Reeb vector field
$M$ be a non-co-Kähler almost co-Kähler 3-manifold such that the Reeb vector field 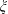 $\unicode[STIX]{x1D709}$ is an eigenvector field of the Ricci operator. If
$\unicode[STIX]{x1D709}$ is an eigenvector field of the Ricci operator. If 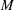 $M$ is a Ricci soliton with transversal potential vector field, then it is locally isometric to Lie group
$M$ is a Ricci soliton with transversal potential vector field, then it is locally isometric to Lie group 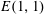 $E(1,1)$ of rigid motions of the Minkowski 2-space.
$E(1,1)$ of rigid motions of the Minkowski 2-space.



