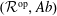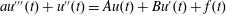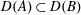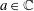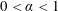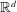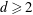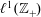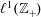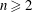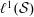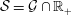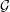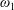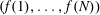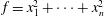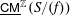Article
On Differential Torsion Theories and Rings with Several Objects
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 703-714
-
- Article
- Export citation
Well-posedness of Third Order Differential Equations in Hölder Continuous Function Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2018, pp. 715-726
-
- Article
- Export citation
Topological Properties of a Class of Higher-dimensional Self-affine Tiles
- Part of:
-
- Published online by Cambridge University Press:
- 03 May 2019, pp. 727-740
-
- Article
- Export citation
Diameter, Decomposability, and Minkowski Sums of Polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2018, pp. 741-755
-
- Article
- Export citation
Simplicial (Co)-homology of
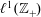 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2018, pp. 756-766
-
- Article
- Export citation
Universal Entire Functions That Define Order Isomorphisms of Countable Real Sets
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2019, pp. 767-779
-
- Article
- Export citation
Perturbation Analysis of Orthogonal Least Squares
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2019, pp. 780-797
-
- Article
- Export citation
Sidon Sets are Proportionally Sidon with Small Sidon Constants
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2018, pp. 798-809
-
- Article
- Export citation
Rings whose Elements are the Sum of a Tripotent and an Element from the Jacobson Radical
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2019, pp. 810-821
-
- Article
- Export citation
Einstein–Maxwell Equations on Four-dimensional Lie Algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 May 2019, pp. 822-840
-
- Article
- Export citation
The Shifted Turán Sieve Method on Tournaments
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 841-855
-
- Article
- Export citation
Chains of P-points
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 856-868
-
- Article
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
-
- Article
- Export citation
Büchi’s Problem in Modular Arithmetic for Arbitrary Quadratic Polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2019, pp. 876-885
-
- Article
- Export citation
Linear Conjugacy
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 886-895
-
- Article
- Export citation
On Knörrer Periodicity for Quadric Hypersurfaces in Skew Projective Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2018, pp. 896-911
-
- Article
- Export citation
Ricci Solitons on Almost Co-Kähler Manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2018, pp. 912-922
-
- Article
- Export citation
Multiple Lattice Tilings in Euclidean Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 923-929
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
BCM volume 62 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 November 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
BCM volume 62 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 November 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation