Research Article
Sur Quelques Series de Lambert et de Dirichlet
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-19
-
- Article
-
- You have access
- Export citation
Power Series Representing Certain Rational Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 20-26
-
- Article
-
- You have access
- Export citation
Certain Bilateral Hypergeometric Identities Of Cayley And Orr Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-39
-
- Article
-
- You have access
- Export citation
On Connections Between Growth and Distribution of Zeros of Integral Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-44
-
- Article
-
- You have access
- Export citation
A Cosine Functional Equation in Hilbert Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-50
-
- Article
-
- You have access
- Export citation
Sheets of Real Analytic Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 51-67
-
- Article
-
- You have access
- Export citation
On Finite Nilpotent Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 68-72
-
- Article
-
- You have access
- Export citation
Finite Groups Which Admit An Automorphism With Few Orbits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-100
-
- Article
-
- You have access
- Export citation
Sur le Radical Corpoïdal D'un Anneau
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 101-106
-
- Article
-
- You have access
- Export citation
On Representations of Orders Over Dedekind Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-125
-
- Article
-
- You have access
- Export citation
Integral p-adic Normal Matrices Satisfying the Incidence Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 126-133
-
- Article
-
- You have access
- Export citation
Loops with Adjoints
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-144
-
- Article
-
- You have access
- Export citation
On Quadruple Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-157
-
- Article
-
- You have access
- Export citation
A Metrization for Power-Sets with Applications to Combinatorial Analysis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 158-176
-
- Article
-
- You have access
- Export citation
On the Composition of Balanced Incomplete Block Designs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 177-188
-
- Article
-
- You have access
- Export citation
Further Results on the Construction of Mutually Orthogonal Latin Squares and the Falsity of Euler's Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 189-203
-
- Article
-
- You have access
- Export citation
On the Maximal Number of Pairwise Orthogonal Latin Squares of a Given Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-208
-
- Article
-
- You have access
- Export citation
A Simple Closed Curve is the Only Homogeneous Bounded Plane Continuum that Contains an Arc
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-230
-
- Article
-
- You have access
- Export citation
Sur La Cohomologie Non Abelienne I (Dimension Deux)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-251
-
- Article
-
- You have access
- Export citation
On Homeomorphisms between Extension Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-262
-
- Article
-
- You have access
- Export citation

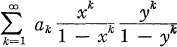
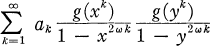
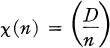
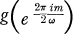
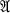 denote the set of functions of a complex variable
denote the set of functions of a complex variable 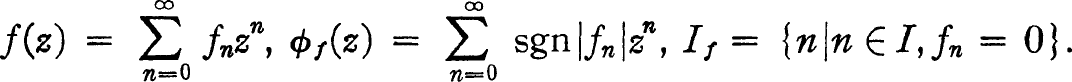
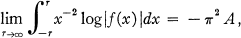
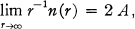

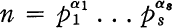
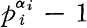
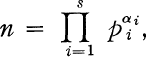
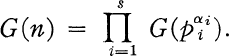
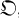 , that is, of o-regular
, that is, of o-regular 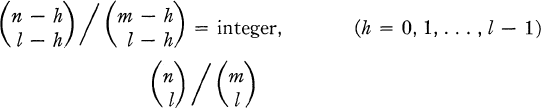
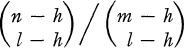

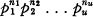
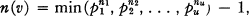
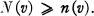
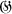 de groupes non abéliens est liée à la classification de certains types d'espaces fibres principaux de base
de groupes non abéliens est liée à la classification de certains types d'espaces fibres principaux de base