Article contents
On Connections Between Growth and Distribution of Zeros of Integral Functions
Published online by Cambridge University Press: 20 November 2018
Extract
The following theorem was proved by Paley and Wiener (4, p. 70; 1, p. 136).
Theorem 1. If f(z) is a canonical product of order 1 with real zeros, and f(0) = 1, the conditions
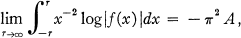
and
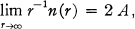
are equivalent. n(r) denotes the number of zeros of absolute value not exceeding r.
Instead of assuming the zeros to be all real Pfluger assumed that the zeros are close to the real axis and proved the following theorem (5 or 1, p. 143).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1960
References
- 1
- Cited by


