Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-19T19:41:51.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur La Cohomologie Non Abelienne I (Dimension Deux)

Published online by Cambridge University Press:  20 November 2018

Paul Dedecker
Paul Dedecker*
Affiliation:
Université de Liège Istituto Matematico Dell' Università di Roma
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On sait que la définition de la cohomologie d'un espace X à coefficients dans un faisceau de groupes non abéliens est liée à la classification de certains types d'espaces fibres principaux de base X (1; 8; 10). Cette cohomologie se définit assez facilement en dimensions zéro et un, mais pour certains problèmes, il serait utile de pouvoir la définir en dimension deux également.

J'ai abordé la question dans (3; 6) mais un certain nombre de difficultés subsistaient qu'il semble utile de chercher à éliminer, ce qui est l'objet de la présente note.

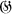Remarquons d'abord que la définition de H°(X, ), groupe des sections de 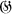, est triviale, aucune difficulté ne résultant du caractère non abélien de 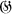. En ce qui concerne H1(X, 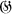) une difficulté naît du fait que cet ensemble n'est plus un groupe, même non abélien; il possède toutefois un élément neutre privilégié.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 231 - 251
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Dedecker, P., Jets locaux, faisceaux, germes de sous-espaces, Bull. Soc. Math. Belg., 6 (1953- 4), 119.Google Scholar
2. Dedecker, P., Extension du groupe structural d'un espace fibre, Colloque de topologie de Strasbourg (mai 1955).Google Scholar
3. Dedecker, P., Cohomologie à coefficients non abêliens et espaces fibres, Bull. Acad. Roy. Belg., 41 (1955), 1132–1146.Google Scholar
4. Dedecker, P., La structure algébrique de Vensemble des classes fibres, Bull Acad. Roy. Belg., 42 (1956), 270–290.Google Scholar
5. Dedecker, P., Groupoïdes de cohomologie à coefficients non abêliens et espaces fibres, Colloque de topologie algébrique, Louvain, C.B.R.M. (1956).Google Scholar
6. Dedecker, P., On the exact cohomology sequence of a space with coefficients in a non abelien sheaf. International Symposium on Algebraic Topology, Mexico (1956), à paraître.Google Scholar
7. Dedecker, P., Cohomologie de dimension 2 à coefficients non abêliens, Comptes rendus, Paris, 247 (1958).Google Scholar
8. Frenkel, J., Sur une classe d'espaces fibres analytiques, Comptes rendus, Paris, 236 (1953), 40–41.Google Scholar
9. Frenkel, J., Cohomologie à coefficients dans un faisceau non abêlien, Comptes rendus, Paris, 240 (1957), 2368–2370.Google Scholar
10. Frenkel, J., Cohomologie non abêlienne et espaces fibres, Bull. Soc. Math. France, 85 (1957), 135–220.Google Scholar
11. Grothendieck, A., A general theory of fibre spaces with structure sheaf, University of Kansas, N.S.F. Report No. 4 (August, 1955).Google Scholar