Research Article
Matrix Rational Completions Satisfying Generalized Incidence Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-12
-
- Article
-
- You have access
- Export citation
Derivative of Singular Set-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-16
-
- Article
-
- You have access
- Export citation
A General Perron Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-30
-
- Article
-
- You have access
- Export citation
A Class of Translation Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-39
-
- Article
-
- You have access
- Export citation
Semigroups Co-Ordinatizing Orthomodular Geometries
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 40-51
-
- Article
-
- You have access
- Export citation
Semigroups in Which all Subsemigroups are Left Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-62
-
- Article
-
- You have access
- Export citation
A Property of Two Chords which Divide a Convex Curve into Four Arcs of Equal Length
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-77
-
- Article
-
- You have access
- Export citation
Identities of Non-Associative Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 78-92
-
- Article
-
- You have access
- Export citation
On the Total Area of the Faces Of a Four-Dimensional Polytope
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-99
-
- Article
-
- You have access
- Export citation
A Census of Finite Automata
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-113
-
- Article
-
- You have access
- Export citation
Some Configurations in Finite Projective Spaces and Partially Balanced Incomplete Block Designs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-123
-
- Article
-
- You have access
- Export citation
On Generalized Powers of the Difference Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 124-129
-
- Article
-
- You have access
- Export citation
An Extension of the Class of Alternative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-141
-
- Article
-
- You have access
- Export citation
Fubini Theorem For a Certain Type of Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 142-154
-
- Article
-
- You have access
- Export citation
Completions of Quadrangles in Projective Planes II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 155-165
-
- Article
-
- You have access
- Export citation
Some Properties of Graphs with Multiple Edges
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-177
-
- Article
-
- You have access
- Export citation
Ideal Decompositions in Noetherian Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 178-184
-
- Article
-
- You have access
- Export citation
A Distortion Theorem for Analytic Maps of Annuli
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-198
-
- Article
-
- You have access
- Export citation
Anneaux Métaprimitifs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 199-205
-
- Article
-
- You have access
- Export citation
Uniform and Equicontinuous Schauder Bases of Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 207-212
-
- Article
-
- You have access
- Export citation



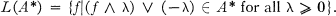
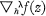 for arbitrary real λ and
for arbitrary real λ and 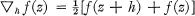
 by means of a suitable projection map p. Since this covering map is not unique, it seems natural to single out some such maps by an extremal property. The use of Riemannian metrics compatible with the conformai structure on the given surface
by means of a suitable projection map p. Since this covering map is not unique, it seems natural to single out some such maps by an extremal property. The use of Riemannian metrics compatible with the conformai structure on the given surface  for the study of $1 is well known ; from the point of view of differential geometry it suggests an investigation of the distortion caused by
for the study of $1 is well known ; from the point of view of differential geometry it suggests an investigation of the distortion caused by