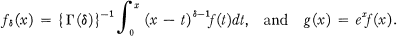Research Article
Averaging Operators and C(X)-Spaces with the Separable Projection Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-904
-
- Article
-
- You have access
- Export citation
Limit Point and Limit Circle Criteria for a Class of Singular Symmetric Differential Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 905-914
-
- Article
-
- You have access
- Export citation
Rings With Involution Whose Symmetric Units Commute
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 915-928
-
- Article
-
- You have access
- Export citation
More About the Mathieu Group M22
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-937
-
- Article
-
- You have access
- Export citation
Weierstrass Division in Quasianalytic Local Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 938-953
-
- Article
-
- You have access
- Export citation
Integral Group Rings with Nilpotent Unit Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 954-960
-
- Article
-
- You have access
- Export citation
Sur L'Approximation Polynomiale Sur Tout L'axe Reel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-967
-
- Article
-
- You have access
- Export citation
The Algebraic Independence of Certain Exponential Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 968-976
-
- Article
-
- You have access
- Export citation
Free Ortholattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 977-985
-
- Article
-
- You have access
- Export citation
A Commutativity Condition for Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 986-991
-
- Article
-
- You have access
- Export citation
Two More Hereditarily Separable Non-Lindelöf Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 998-1005
-
- Article
-
- You have access
- Export citation
Some Fixed Point Theorems for Partially Ordered Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 992-997
-
- Article
-
- You have access
- Export citation
Amicable Orthogonal Designs-Existence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1006-1020
-
- Article
-
- You have access
- Export citation
Some Geometries Associated with Parabolic Representations of Groups of Lie Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1021-1031
-
- Article
-
- You have access
- Export citation
Cyclic Element Theory in Connected and Locally Connected Hausdorff Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1032-1050
-
- Article
-
- You have access
- Export citation
A Decomposition Theorem for m-Convex Sets in Rd
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1051-1057
-
- Article
-
- You have access
- Export citation
On Functional Cesàro And Hölder Methods of Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1058-1061
-
- Article
-
- You have access
- Export citation
A Lattice-Theoretic Description of the Lattice of Hyperinvariant Subspaces of a Linear Transformation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1062-1066
-
- Article
-
- You have access
- Export citation
On Jordan Structure in Semiprime Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1072
-
- Article
-
- You have access
- Export citation
A Simple Proof of the Maximal Ergodic Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1073-1075
-
- Article
-
- You have access
- Export citation



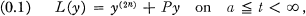
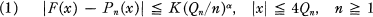
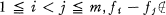 , C
, C 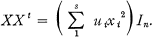
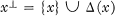 . Let (G,
. Let (G, 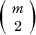 line segments determined by these points lies in
line segments determined by these points lies in