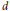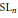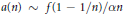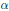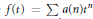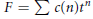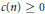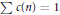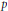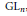Research Article
Distributions invariantes sur les groupes réductifs quasi-déployés
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-999
-
- Article
-
- You have access
- Export citation
On the Cohomology of Moduli of Vector Bundles and the Tamagawa Number of SLn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1000-1025
-
- Article
-
- You have access
- Export citation
Karamata Renewed and Local Limit Results
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1026-1094
-
- Article
-
- You have access
- Export citation
A Casselman–Shalika Formula for the Shalika Model of GLn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1095-1120
-
- Article
-
- You have access
- Export citation