Research Article
Certain Artinian Rings are Noetherian
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 553-556
-
- Article
-
- You have access
- Export citation
Rings with Finite Norm Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 557-565
-
- Article
-
- You have access
- Export citation
Radicals of PID's and Dedekind Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 566-572
-
- Article
-
- You have access
- Export citation
Galois Theory of Essential Extensions of Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-579
-
- Article
-
- You have access
- Export citation
Normed Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 580-591
-
- Article
-
- You have access
- Export citation
Representation of Algebras with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 592-597
-
- Article
-
- You have access
- Export citation
Restrictive Semigroups of Continuous Functions on 0-Dimensional Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-611
-
- Article
-
- You have access
- Export citation
Riemann Surfaces as Orbit Spaces of Fuchsian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 612-616
-
- Article
-
- You have access
- Export citation
Abelian Groups Quasi-Injective Over their Endomorphism Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 617-621
-
- Article
-
- You have access
- Export citation
Nowhere Dense Subsets of Metric Spaces with Applications to Stone-Cech Compactifications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 622-630
-
- Article
-
- You have access
- Export citation
δ-Continuous Selections of Small Multifunction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 631-635
-
- Article
-
- You have access
- Export citation
The Extent of the Sequence Space Associated with a Basis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 636-641
-
- Article
-
- You have access
- Export citation
Approximation of Piecewise Continuous Functions by Quotients of Bounded Analytic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 642-657
-
- Article
-
- You have access
- Export citation
The Eigenvalues of Complementary Principal Submatrices of a Positive Definite Matrix
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 658-667
-
- Article
-
- You have access
- Export citation
Separability in an Algebra with Semi-Linear Homomorphism
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 668-671
-
- Article
-
- You have access
- Export citation
A Characterization of the Tits' Simple Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 672-685
-
- Article
-
- You have access
- Export citation
Rational Tensor Representations of Hom(V, V) and an Extension of an Inequality of I. Schur.
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 686-695
-
- Article
-
- You have access
- Export citation
On Scalar Dependent Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-702
-
- Article
-
- You have access
- Export citation
On the Ring of Quotients at a Prime Ideal of a Right Noetherian Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 703-712
-
- Article
-
- You have access
- Export citation
Uniform Finite Generation of SU(2) and SL(2, R)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 713-727
-
- Article
-
- You have access
- Export citation


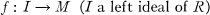
 converges. My primary motivation in writing this paper was to present a new proof to a recent theorem of N. I. and V. I. Gurarii concerning limits of extent on
converges. My primary motivation in writing this paper was to present a new proof to a recent theorem of N. I. and V. I. Gurarii concerning limits of extent on 

 denote the eigenvalues of
denote the eigenvalues of 

 of index 2. In this paper we prove the following theorem:
of index 2. In this paper we prove the following theorem: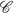 (P).
(P).