Research Article
Nilpotent Extensions of Abelian p-GROUPS
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1025-1052
-
- Article
-
- You have access
- Export citation
On Periodicity in Topological Surgery
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1053-1064
-
- Article
-
- You have access
- Export citation
The Tensor Product of Operational Logics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1065-1080
-
- Article
-
- You have access
- Export citation
A Voronovskaya Theorem for Variation-Diminishing Spline Approximation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1081-1093
-
- Article
-
- You have access
- Export citation
A Family of M*-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1094-1109
-
- Article
-
- You have access
- Export citation
Classification of Algebraic Surfaces with Sectional Genus less than or Equal to Six. II: Ruled Surfaces with dim ϕKx⊗L(x) = l
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1110-1121
-
- Article
-
- You have access
- Export citation
Homomorphisms of Distributive Lattices as Restrictions of Congruences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1122-1134
-
- Article
-
- You have access
- Export citation
On the Spectra of Unbounded Subnormal Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1135-1148
-
- Article
-
- You have access
- Export citation
Porosity and Approximate Derivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1149-1180
-
- Article
-
- You have access
- Export citation
Distance Functions and Orlicz-Sobolev Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1181-1198
-
- Article
-
- You have access
- Export citation
Sufficiency and the Jacobi Condition in the Calculus of Variations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1199-1209
-
- Article
-
- You have access
- Export citation
(0, 2) – Interpolation of Entire Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1210-1227
-
- Article
-
- You have access
- Export citation
The Ideal Generation Conjecture for 28 Points in P3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1228-1238
-
- Article
-
- You have access
- Export citation
Excising States of C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1239-1260
-
- Article
-
- You have access
- Export citation
Four Integers whose Twelve Quotients Sum to Zero
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1261-1280
-
- Article
-
- You have access
- Export citation

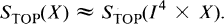
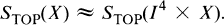
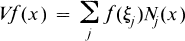

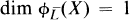 where
where 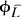 is the map associated to
is the map associated to 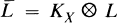 . L. Roth in [
. L. Roth in [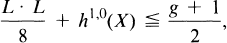
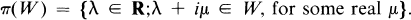
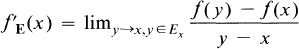
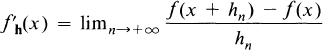
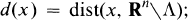
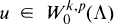 . Further results in this direction are given in [
. Further results in this direction are given in [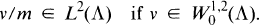
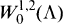 may in this case be characterized as the subspace of
may in this case be characterized as the subspace of 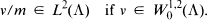
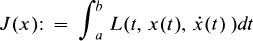
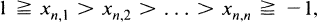
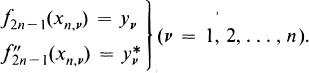
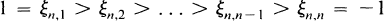

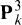 , (
, (