Research Article
The Real Spectrum of Higher Level of a Commutative Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-462
-
- Article
-
- You have access
- Export citation
Decomposition of Multivariate Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-482
-
- Article
-
- You have access
- Export citation
Slicings, Selections and Their Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-504
-
- Article
-
- You have access
- Export citation
Extreme and Exposed Points in Orlicz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 505-515
-
- Article
-
- You have access
- Export citation
Primitivity in Free Groups and Free Metabelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 516-523
-
- Article
-
- You have access
- Export citation
A Segal-Langevin Type Stochastic Differential Equation on a Space Of Generalized Functionals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 524-552
-
- Article
-
- You have access
- Export citation
Lie Ideals and Central Identities With Derivation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 553-560
-
- Article
-
- You have access
- Export citation
Hermite and Hermite-Fejer Interpolation and Associated Product Integration Rules on the Real Line: The L1 Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-590
-
- Article
-
- You have access
- Export citation
Sk2 and K3 Of Dihedral Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 591-623
-
- Article
-
- You have access
- Export citation
The Heat Equation on the Spaces of Positive Definite Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 624-651
-
- Article
-
- You have access
- Export citation
Fixed Point Theorems for Measurable Semigroups of Operations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 652-664
-
- Article
-
- You have access
- Export citation
The Structure of Schur Algebras Sk(n, p) for n ≥ p
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 665-672
-
- Article
-
- You have access
- Export citation



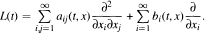
 which transforms functions of compact support on an euclidean space into integrable functions on the symmetric space. The transform
which transforms functions of compact support on an euclidean space into integrable functions on the symmetric space. The transform  is the usual Laplacian with a constant drift).
is the usual Laplacian with a constant drift).