Research Article
Discrete Subsets of Proximity Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-230
-
- Article
-
- You have access
- Export citation
The Density of Zeros of Dirichlet's L-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-240
-
- Article
-
- You have access
- Export citation
A Note on the Normal Moore Space Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-251
-
- Article
-
- You have access
- Export citation
On Counting Types of Symmetries in Finite Unitary Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-254
-
- Article
-
- You have access
- Export citation
On Global Inverse Theorems of Szász and Baskakov Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-263
-
- Article
-
- You have access
- Export citation
Criteres de G-Stabilite en Termes de Transversalite
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 264-273
-
- Article
-
- You have access
- Export citation
On Certain Polynomials of Gaussian Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 274-281
-
- Article
-
- You have access
- Export citation
α-Speedable and non α-Speedable Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-299
-
- Article
-
- You have access
- Export citation
The Schur Subgroup of a p-Adic Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 300-303
-
- Article
-
- You have access
- Export citation
Compatible Tight Riesz Orders II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 304-307
-
- Article
-
- You have access
- Export citation
Solvable Subgroups and their Lie Algebras in Characteristic p
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 308-311
-
- Article
-
- You have access
- Export citation
An Alternative Approach to Laguerre Polynomial Identities in Combinatorics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-319
-
- Article
-
- You have access
- Export citation
Classification of Finite Spaces of Orderings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-330
-
- Article
-
- You have access
- Export citation
The Unrestricted Section Properties of Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 331-336
-
- Article
-
- You have access
- Export citation
A Semilinear Dirichlet Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-340
-
- Article
-
- You have access
- Export citation
A Measure of Linear Independence for Some Exponential Functions II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 341-346
-
- Article
-
- You have access
- Export citation
On Bernstein's Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-353
-
- Article
-
- You have access
- Export citation
Factorization of Affinities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-362
-
- Article
-
- You have access
- Export citation
Stable Homeomorphisms of the Pseudo-Arc
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-374
-
- Article
-
- You have access
- Export citation
L'isolateur D'Un Homomorphisme de Groupes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 375-391
-
- Article
-
- You have access
- Export citation

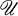 for
for 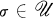 where
where 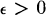 if
if  , for all
, for all 

 denotes any fixed positive quantity.
denotes any fixed positive quantity.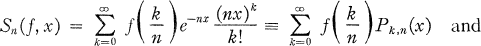
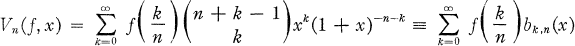
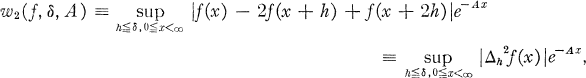
 l'anneau des germes en 0 des fonctions numériques de classe
l'anneau des germes en 0 des fonctions numériques de classe  de la structure de groupe définie par la multiplication:
de la structure de groupe définie par la multiplication:
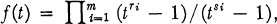

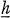 denotes the Lie algebra of
denotes the Lie algebra of  is the Lie algebra
is the Lie algebra 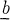 of some Borel subgroup
of some Borel subgroup 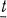 of some maximal torus
of some maximal torus 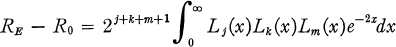
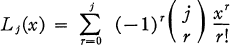
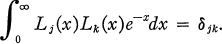
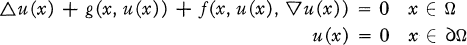
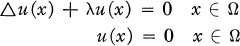
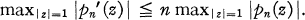
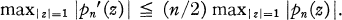
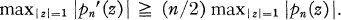
 la catégorie des groupes localement nilpotents.
la catégorie des groupes localement nilpotents.