Research Article
On the Existence of Normal Metacompact Moore Spaces which are not Metrizable
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-6
-
- Article
-
- You have access
- Export citation
Which Abelian Groups Can be Fundamental Groups of Regions in Euclidean Spaces?
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 7-18
-
- Article
-
- You have access
- Export citation
Absolute Tauberian Constants for Hausdorff Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-26
-
- Article
-
- You have access
- Export citation
An Intermediate Value Property for Operators with Applications to Integral and Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-41
-
- Article
-
- You have access
- Export citation
The Primitive Ideal Space of a C*-Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 42-49
-
- Article
-
- You have access
- Export citation
Enumerating Dissectible Polyhedra by Their Automorphism Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-67
-
- Article
-
- You have access
- Export citation
On the Splitting of Modules and Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 68-77
-
- Article
-
- You have access
- Export citation
Rank r Solutions to the Matrix Equation XAXT = C, A Nonalternate, C Alternate, Over GF(2y).
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 78-90
-
- Article
-
- You have access
- Export citation
The Banach-Saks Theorem in C(S)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 91-97
-
- Article
-
- You have access
- Export citation
Prime Ideals in GCD-Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 98-107
-
- Article
-
- You have access
- Export citation
A Dimension Theorem for Real Primes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 108-114
-
- Article
-
- You have access
- Export citation
Operators with Compact Self-Commutator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-120
-
- Article
-
- You have access
- Export citation
Some Results on Semi-Perfect Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 121-129
-
- Article
-
- You have access
- Export citation
Rings with Involution in which Every Trace is Nilpotent or Regular
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 130-137
-
- Article
-
- You have access
- Export citation
A Generalization of Thom Classes and Characteristic Classes to Nonspherical Fibrations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 138-144
-
- Article
-
- You have access
- Export citation
Double Covers and Metastable Immersions of Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-176
-
- Article
-
- You have access
- Export citation
On Going Down in Polynomial Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 177-184
-
- Article
-
- You have access
- Export citation
Some C*-Algebras with Outer Derivations, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-189
-
- Article
-
- You have access
- Export citation
Chains of Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-206
-
- Article
-
- You have access
- Export citation
Entire Functions with Some Derivatives Univalent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 207-213
-
- Article
-
- You have access
- Export citation

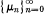 be a fixed sequence of real or complex numbers. The Hausdorff transform {
be a fixed sequence of real or complex numbers. The Hausdorff transform {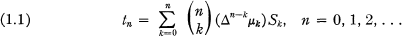
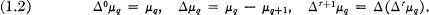
 -free if each subgroup of rank less than
-free if each subgroup of rank less than 
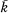 be an algebraic closure of
be an algebraic closure of 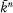 (n some integer greater than 0) which is the set of zeros of some polynomials in
(n some integer greater than 0) which is the set of zeros of some polynomials in 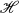 be a fixed separable, infinite dimensional complex Hilbert space, and let
be a fixed separable, infinite dimensional complex Hilbert space, and let  (
( and the canonical quotient map from
and the canonical quotient map from  is a variety of groups that can be denned by
is a variety of groups that can be denned by  where
where  is the variety of nilpotent-of-class-
is the variety of nilpotent-of-class- is the abelian variety and
is the abelian variety and  is the variety of centre-bymetabelian groups. For
is the variety of centre-bymetabelian groups. For  the inclusions are likewise proper but for
the inclusions are likewise proper but for  the corresponding chain is:
the corresponding chain is: 
 is a strictly-increasing sequence of positive integers such that each f
is a strictly-increasing sequence of positive integers such that each f