Article contents
Chains of Varieties
Published online by Cambridge University Press: 20 November 2018
Summary
If 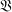 is a variety of groups that can be denned by n-variable laws and
is a variety of groups that can be denned by n-variable laws and 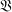 (m) is the variety all of whose m-generator groups are in
(m) is the variety all of whose m-generator groups are in 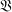 then there corresponds the chain:
then there corresponds the chain: 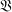 (1) ≧
(1) ≧ 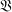 (2) ≧ . . . ≧
(2) ≧ . . . ≧ 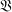 (n) =
(n) = 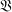 . In this paper such chains are investigated to determine which of the inclusions are proper for certain varieties
. In this paper such chains are investigated to determine which of the inclusions are proper for certain varieties 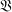 . In particular the inclusions are shown to be all proper for the varieties
. In particular the inclusions are shown to be all proper for the varieties 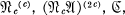 where
where 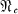 is the variety of nilpotent-of-class-c groups,
is the variety of nilpotent-of-class-c groups, 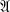 is the abelian variety and
is the abelian variety and 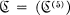 is the variety of centre-bymetabelian groups. For
is the variety of centre-bymetabelian groups. For 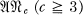 the inclusions are likewise proper but for
the inclusions are likewise proper but for 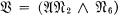 the corresponding chain is:
the corresponding chain is: 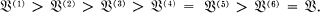
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
- 1
- Cited by


