Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T17:39:50.601Z Has data issue: false hasContentIssue false
  • English
  • Français

Operators with Compact Self-Commutator

Published online by Cambridge University Press:  20 November 2018

Carl Pearcy  and
Norberto Salinas
Carl Pearcy
Affiliation:
University of Michigan, Ann Arbor, Michigan; The Institute for Advanced Study, Princeton, New Jersey; University of Kansas, Lawrence, Kansas
Norberto Salinas
Affiliation:
University of Michigan, Ann Arbor, Michigan; The Institute for Advanced Study, Princeton, New Jersey; University of Kansas, Lawrence, Kansas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

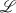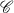Let be a fixed separable, infinite dimensional complex Hilbert space, and let () denote the algebra of all (bounded, linear) operators on . The ideal of all compact operators on will be denoted by and the canonical quotient map from 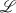() onto the Calkin algebra 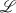()/ 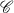will be denoted by π.

Some open problems in the theory of extensions of C*-algebras (cf. [1]) have recently motivated an increasing interest in the class of all operators in 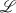() whose self-commuta tor is compact.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 115 - 120
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Douglas, R. G., Banach algebras techniques in the theory of Toeplitz operators, lectures given in the CBMS Regional Conference at the University of Georgia, June 12-16, 1972.Google Scholar
2. Douglas, R. G. and C. Pearcy, A note on quasitriangular operators, Duke Math. J. 37 (1970), 177–188.Google Scholar
3. Halmos, P. R., Ten problems in Hilbert space, Bull. Amer. Math. Soc. 76 (1970), 887–933.Google Scholar
4. Halmos, P. R., Continuous functions of Hermitian operators, Proc. Amer. Math. Soc. 81 (1972), 130–132.Google Scholar
5. Lancaster, John S., Lifting from the Calkin Algebra, Ph.D. thesis, Indiana University, 1972.Google Scholar
6. Sikonia, W., The von Neumann converse of WeyVs Theorem, Indiana Univ. Math. J. 21 (1971), 121–123.Google Scholar