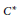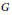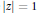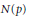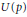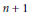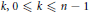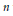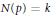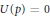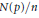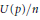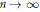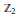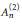Research Article
The C*–algebras of Compact Transformation Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-506
-
- Article
-
- You have access
- Export citation
On Littlewood Polynomials with Prescribed Number of Zeros Inside the Unit Disk
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-526
-
- Article
-
- You have access
- Export citation
Obstructions to Approximating Tropical Curves in Surfaces Via Intersection Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 527-572
-
- Article
-
- You have access
- Export citation
Twisted Vertex Operators and Unitary Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-596
-
- Article
-
- You have access
- Export citation
Sommes friables d'exponentielles et applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 597-638
-
- Article
-
- You have access
- Export citation
Projectivity in Algebraic Cobordism
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 639-653
-
- Article
-
- You have access
- Export citation
Growth of Selmer Groups of CM Abelian Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 654-666
-
- Article
-
- You have access
- Export citation
Toric Degenerations, Tropical Curve, and Gromov–Witten Invariants of Fano Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 667-695
-
- Article
-
- You have access
- Export citation
Geography of Irregular Gorenstein 3–folds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-720
-
- Article
-
- You have access
- Export citation