No CrossRef data available.
Article contents
Galois Module Structure of Ambiguous Ideals in Biquadratic Extensions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 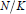 $N/K$ be a biquadratic extension of algebraic number fields, and
$N/K$ be a biquadratic extension of algebraic number fields, and 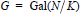 $G\,=\,\text{Gal(}N/K\text{)}$. Under a weak restriction on the ramification filtration associated with each prime of
$G\,=\,\text{Gal(}N/K\text{)}$. Under a weak restriction on the ramification filtration associated with each prime of 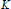 $K$ above 2, we explicitly describe the
$K$ above 2, we explicitly describe the 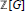 $\mathbb{Z}\text{ }[G]\text{ }$-module structure of each ambiguous ideal of
$\mathbb{Z}\text{ }[G]\text{ }$-module structure of each ambiguous ideal of 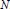 $N$. We find under this restriction that in the representation of each ambiguous ideal as a
$N$. We find under this restriction that in the representation of each ambiguous ideal as a 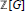 $\mathbb{Z}\text{ }[G]\text{ }$-module, the exponent (or multiplicity) of each indecomposable module is determined by the invariants of ramification, alone.
$\mathbb{Z}\text{ }[G]\text{ }$-module, the exponent (or multiplicity) of each indecomposable module is determined by the invariants of ramification, alone.
For a given group, 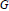 $G$, define
$G$, define  ${{S}_{G}}$ to be the set of indecomposable
${{S}_{G}}$ to be the set of indecomposable 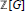 $\mathbb{Z}\text{ }[G]\text{ }$-modules,
$\mathbb{Z}\text{ }[G]\text{ }$-modules, 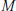 $M$, such that there is an extension,
$M$, such that there is an extension, 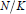 $N/K$, for which
$N/K$, for which 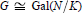 $G\cong \text{Gal(}N/K\text{)}$, and
$G\cong \text{Gal(}N/K\text{)}$, and 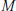 $M$ is a
$M$ is a 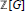 $\mathbb{Z}\text{ }[G]\text{ }$-module summand of an ambiguous ideal of
$\mathbb{Z}\text{ }[G]\text{ }$-module summand of an ambiguous ideal of 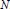 $N$. Can
$N$. Can 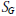 ${{S}_{G}}$ ever be infinite? In this paper we answer this question of Chinburg in the affirmative.
${{S}_{G}}$ ever be infinite? In this paper we answer this question of Chinburg in the affirmative.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998




