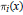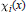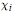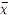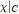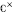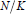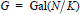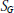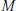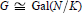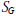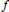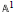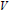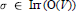Research Article
Fourier Multipliers For Local Hardy Spaces On Chébli-Trimèche Hypergroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-928
-
- Article
-
- You have access
- Export citation
Decomposition Varieties in Semisimple Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-971
-
- Article
-
- You have access
- Export citation
Trace Class Elements and Cross-Sections in Kac-Moody Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 972-1006
-
- Article
-
- You have access
- Export citation
Galois Module Structure of Ambiguous Ideals in Biquadratic Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1007-1047
-
- Article
-
- You have access
- Export citation
Localization Theories for Simplicial Presheaves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1048-1089
-
- Article
-
- You have access
- Export citation
Sur les Transformées de Riesz sur les Groupes de Lie Moyennables et sur Certains Espaces Homogènes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1090-1104
-
- Article
-
- You have access
- Export citation
Tempered Representations and the Theta Correspondence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1105-1118
-
- Article
-
- You have access
- Export citation