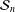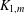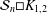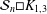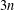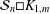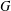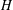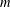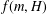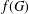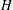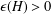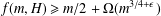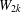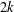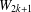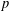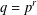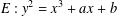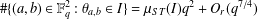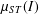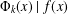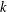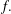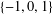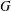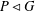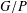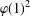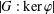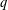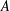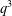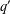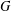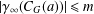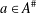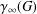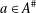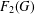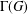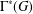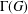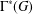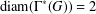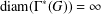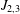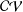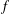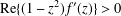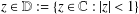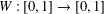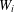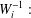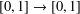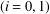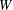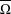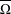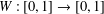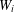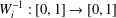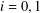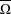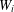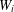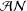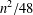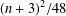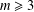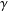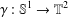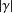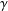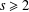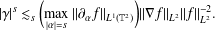Editorial
EDITORIAL: A CENTENARY OF THE BULLETIN OF THE AUSTRALIAN MATHEMATICAL SOCIETY
-
- Published online by Cambridge University Press:
- 05 July 2019, pp. 1-4
-
- Article
-
- You have access
- Export citation
Research Article
ON THE CROSSING NUMBER OF THE CARTESIAN PRODUCT OF A SUNLET GRAPH AND A STAR GRAPH
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2019, pp. 5-12
-
- Article
- Export citation
MAXIMUM CUTS IN GRAPHS WITHOUT WHEELS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 13-26
-
- Article
- Export citation
THE ERROR TERM IN THE SATO–TATE THEOREM OF BIRCH
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2019, pp. 27-33
-
- Article
- Export citation
ANALOGUES OF THE AOKI–OHNO AND LE–MURAKAMI RELATIONS FOR FINITE MULTIPLE ZETA VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 34-40
-
- Article
- Export citation
CYCLOTOMIC FACTORS OF BORWEIN POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2019, pp. 41-47
-
- Article
- Export citation
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
-
- Article
- Export citation
SQUARES OF DEGREES OF BRAUER CHARACTERS AND MONOMIAL BRAUER CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 58-60
-
- Article
- Export citation
FITTING SUBGROUP AND NILPOTENT RESIDUAL OF FIXED POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 61-67
-
- Article
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
-
- Article
- Export citation
ON GENERATORS AND DISTURBANCES OF DYNAMICAL SYSTEMS IN THE CONTEXT OF CHAOTIC POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 76-85
-
- Article
- Export citation
SHARP BOUNDS OF SOME COEFFICIENT FUNCTIONALS OVER THE CLASS OF FUNCTIONS CONVEX IN THE DIRECTION OF THE IMAGINARY AXIS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 86-96
-
- Article
- Export citation
SYMMETRIC ITINERARY SETS
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2019, pp. 97-108
-
- Article
- Export citation
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 109-118
-
- Article
- Export citation
A CHARACTERISATION OF TRACIALLY NUCLEAR C*-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 119-128
-
- Article
- Export citation
A NOTE ON POSITIVE
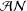 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 129-130
-
- Article
- Export citation
INTEGER POLYGONS OF GIVEN PERIMETER
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 131-147
-
- Article
- Export citation
A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 148-154
-
- Article
- Export citation
SPACES OF SPECIAL QUADRILATERALS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 155-167
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
GEOMETRY OF INTEGRABLE LATTICE EQUATIONS AND THEIR REDUCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 168-169
-
- Article
-
- You have access
- Export citation