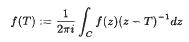Research Article
Equality algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-191
-
- Article
-
- You have access
- Export citation
On a Banach space without a weak mid-point locally uniformly rotund norm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-196
-
- Article
-
- You have access
- Export citation
Systems of differential equations with fully nonlinear boundary conditions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-208
-
- Article
-
- You have access
- Export citation
On continuity of derivations and epimorphisms on some vector-valued group algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 209-215
-
- Article
-
- You have access
- Export citation
Finite element methods for compressible Stokes equations with inflow boundary condition
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 217-225
-
- Article
-
- You have access
- Export citation
Hypersurfaces with special quadric representations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-234
-
- Article
-
- You have access
- Export citation
On conjecture of Resnikoff and Saldaña
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-237
-
- Article
-
- You have access
- Export citation
Canonical point mappings in

-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-242
-
- Article
-
- You have access
- Export citation
A characterisation of cyclic subnormal separated A-groups of nilpotent length three
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-251
-
- Article
-
- You have access
- Export citation
On finite groups with the Cayley invariant property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-261
-
- Article
-
- You have access
- Export citation
Comparable differentiability characterisations of two classes of Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-272
-
- Article
-
- You have access
- Export citation
The computational complexity of torsion-freeness of finitely presented groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-277
-
- Article
-
- You have access
- Export citation
Uniformities and uniformly continuous functions on locally connected groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-283
-
- Article
-
- You have access
- Export citation
Convexité holomorphe intermédiaire des revetements d'un domaine pseudoconvexe
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 285-290
-
- Article
-
- You have access
- Export citation
Quotient de Hadamard en plusieurs variables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-301
-
- Article
-
- You have access
- Export citation
Expansion of analytic functions of an operator in series of Faber polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-318
-
- Article
-
- You have access
- Export citation
Subdifferential Rolle's and mean value inequality theorems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-329
-
- Article
-
- You have access
- Export citation
Fundamental theorem of prehomogeneous vector spaces of characteristic p
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-341
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Partitions into large unequal parts
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-344
-
- Article
-
- You have access
- Export citation
Computational studies of optimal controls
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-347
-
- Article
-
- You have access
- Export citation

 . We use Schauder degree theory in a novel space. Well known existence results for the Picard, the periodic and the Neumann boundary conditions follow as special cases of our results.
. We use Schauder degree theory in a novel space. Well known existence results for the Picard, the periodic and the Neumann boundary conditions follow as special cases of our results.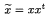 (where
(where 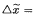
 , where
, where 
 such that
such that  has countable many components onto
has countable many components onto  where
where 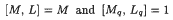
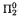 -complete. This implies in particular that there is no effective listing of all torsion-free finitely presented groups, or of all non-torsion-free finitely presented groups.
-complete. This implies in particular that there is no effective listing of all torsion-free finitely presented groups, or of all non-torsion-free finitely presented groups. the covering
the covering  is holomorphically convex with respect to holomorphic sections of
is holomorphically convex with respect to holomorphic sections of  .
.