Research Article
WARPED PRODUCT SEMI-SLANT SUBMANIFOLDS IN LOCALLY RIEMANNIAN PRODUCT MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 177-186
-
- Article
-
- You have access
- Export citation
RIGIDITY OF GRAPH PRODUCTS OF ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 187-196
-
- Article
-
- You have access
- Export citation
LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 197-224
-
- Article
-
- You have access
- Export citation
HIGHER EPISTASIS IN GENETIC ALGORITHMS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 225-243
-
- Article
-
- You have access
- Export citation
MULTIDIMENSIONAL HARDY-TYPE INEQUALITIES VIA CONVEXITY
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 245-260
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF METABELIAN PRIME POWER ORDER GROUPS OF MAXIMAL CLASS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 261-276
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF INDEPENDENT SETS FOR (a,b,k)-CRITICAL GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 277-283
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS FOR A DIRICHLET PROBLEM WITH p-LAPLACIAN AND SET-VALUED NONLINEARITY
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 285-303
-
- Article
-
- You have access
- Export citation
ON R-SECTORIAL DERIVATIVES ON BERGMAN SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 305-313
-
- Article
-
- You have access
- Export citation
CUBIC EDGE-TRANSITIVE GRAPHS OF ORDER 8p2
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 315-323
-
- Article
-
- You have access
- Export citation
APPROXIMATION BY SEVERAL RATIONALS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 325-329
-
- Article
-
- You have access
- Export citation
BOUNDEDNESS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS WITH VARIABLE IMPULSIVE PERTURBATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 331-345
-
- Article
-
- You have access
- Export citation
PhD Thesis
Mathematical modelling of nano-scaled structures, devices and materials
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 347-348
-
- Article
-
- You have access
- Export citation
On E-pseudovarieties of finite regular semigroups
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 349-351
-
- Article
-
- You have access
- Export citation




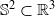 . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set
. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set 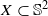 for functions in the Sobolev space
for functions in the Sobolev space 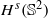 with norm
with norm 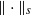 , where
, where 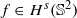 satisfies
satisfies 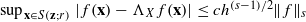 , where
, where 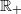 for some positive constants
for some positive constants 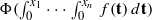 instead of
instead of 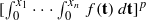 , while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
, while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.