Research Article
ON THE LENGTHS OF PAIRS OF COMPLEX MATRICES OF SIZE SIX
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 177-201
-
- Article
-
- You have access
- Export citation
Addendum
DIAGRAMS OF AN ABELIAN GROUP – ADDENDUM
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. 202-204
-
- Article
-
- You have access
- Export citation
Research Article
SELF-SMALL ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2009, pp. 205-216
-
- Article
-
- You have access
- Export citation
ANNIHILATORS OF POWER VALUES OF GENERALIZED DERIVATIONS ON MULTILINEAR POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2009, pp. 217-232
-
- Article
-
- You have access
- Export citation
THE D-PROPERTY AND THE SORGENFREY LINE
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 233-236
-
- Article
-
- You have access
- Export citation
EIGHT CONSECUTIVE POSITIVE ODD NUMBERS NONE OF WHICH CAN BE EXPRESSED AS A SUM OF TWO PRIME POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 237-243
-
- Article
-
- You have access
- Export citation
COFINITENESS AND FINITENESS OF GENERALIZED LOCAL COHOMOLOGY MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 23 July 2009, pp. 244-250
-
- Article
-
- You have access
- Export citation
A CLASSIFICATION OF SPHERICAL SYMMETRIC CR MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 251-274
-
- Article
-
- You have access
- Export citation
DISCRETENESS CRITERIA FOR MÖBIUS GROUPS ACTING ON
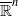 II
II
-
- Published online by Cambridge University Press:
- 19 June 2009, pp. 275-290
-
- Article
-
- You have access
- Export citation
ON p-AUTOMORPHISMS THAT ARE INNER
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 291-293
-
- Article
-
- You have access
- Export citation
SIGN-CHANGING SOLUTIONS FOR A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2009, pp. 294-305
-
- Article
-
- You have access
- Export citation
WEAK BRAIDED BIALGEBRAS AND WEAK ENTWINING STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2009, pp. 306-316
-
- Article
-
- You have access
- Export citation
TRANSITIVITY IN POINT-FREE TOPOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2009, pp. 317-323
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS IN NONHOMOGENEOUS SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2009, pp. 324-334
-
- Article
-
- You have access
- Export citation
REILLY INEQUALITIES OF ELLIPTIC OPERATORS ON CLOSED SUBMANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2009, pp. 335-346
-
- Article
-
- You have access
- Export citation
PhD thesis
SECURE AND PRIVATE FINGERPRINT-BASED AUTHENTICATION
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. 347-349
-
- Article
-
- You have access
- Export citation
Research Article
GENERALIZATIONS OF THE FUNDAMENTAL THEOREM OF PROJECTIVE GEOMETRY
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. 350-352
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 80 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
BAZ volume 80 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 September 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation




 II
II