Let 𝒫 be a Poisson process of intensity 1 in a square Sn of area n. For a fixed integer k, join every point of 𝒫 to its k nearest neighbours, creating an undirected random geometric graph Gn,k. We prove that there exists a critical constant ccrit such that, for c < ccrit, Gn,⌊c log n⌋ is disconnected with probability tending to 1 as n → ∞ and, for c > ccrit, Gn,⌊c log n⌋ is connected with probability tending to 1 as n → ∞. This answers a question posed in Balister et al. (2005).

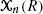Let n points be chosen independently and uniformly in the unit cube [0,1]d, and suppose that each point is supplied with a mark, the marks being independent and identically distributed random variables independent of the location of the points. To each cube R contained in [0,1]d we associate its score defined as the sum of marks of all points contained in 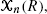R. The scan statistic is defined as the maximum of taken over all cubes R contained in [0,1]d. We show that if the marks are nonlattice random variables with finite exponential moments, having negative mean and assuming positive values with nonzero probability, then the appropriately normalized distribution of the scan statistic converges as n → ∞ to the Gumbel distribution. We also prove a corresponding result for the scan statistic of a Lévy noise with negative mean. The more elementary cases of zero and positive mean are also considered.

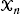Let be a collection of 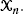n uniform, independent, and identically distributed points on the Cantor ternary set. We consider the asymptotics for the expected total edge length of the directed and undirected nearest-neighbor graph on We prove convergence to a constant of the rescaled expected total edge length of this random graph. The rescaling factor is a function of the fractal dimension and has a log-periodic, nonconstant behavior.

We consider Monte Carlo methods for the classical nonlinear filtering problem. The first method is based on a backward pathwise filtering equation and the second method is related to a backward linear stochastic partial differential equation. We study convergence of the proposed numerical algorithms. The considered methods have such advantages as a capability in principle to solve filtering problems of large dimensionality, reliable error control, and recurrency. Their efficiency is achieved due to the numerical procedures which use effective numerical schemes and variance reduction techniques. The results obtained are supported by numerical experiments.

We study the discrete-time approximation of doubly reflected backward stochastic differential equations (BSDEs) in a multidimensional setting. As in Ma and Zhang (2005) or Bouchard and Chassagneux (2008), we introduce the discretely reflected counterpart of these equations. We then provide representation formulae which allow us to obtain new regularity results. We also propose an Euler scheme type approximation and give new convergence results for both discretely and continuously reflected BSDEs.

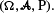Let I1,I2,…,In be independent indicator functions on some probability space We suppose that these indicators can be observed sequentially. Furthermore, let 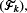T be the set of stopping times on (Ik), k=1,…,n, adapted to the increasing filtration where 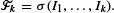The odds algorithm solves the problem of finding a stopping time τ ∈ 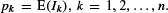T which maximises the probability of stopping on the last Ik=1, if any. To apply the algorithm, we only need the odds for the events {Ik=1}, that is, rk=pk/(1-pk), where The goal of this paper is to offer tractable solutions for the case where the pk are unknown and must be sequentially estimated. The motivation is that this case is important for many real-world applications of optimal stopping. We study several approaches to incorporate sequential information. Our main result is a new version of the odds algorithm based on online observation and sequential updating. Questions of speed and performance of the different approaches are studied in detail, and the conclusiveness of the comparisons allows us to propose always using this algorithm to tackle selection problems of this kind.

In this paper we explore the impact of imitation rules on players' long-run behaviors in evolutionary prisoner's dilemma games. All players sit sequentially and equally spaced around a circle. Players are assumed to interact only with their neighbors, and to imitate either their successful neighbors and/or themselves or the successful actions taken by their neighbors and/or themselves. In the imitating-successful-player dynamics, full defection is the unique long-run equilibrium as the probability of players' experimentations (or mutations) tend to 0. By contrast, full cooperation could emerge in the long run under the imitating-successful-action dynamics. Moreover, it is discovered that the convergence rate to equilibrium under local interaction could be slower than that under global interaction.

In this paper we consider Lévy processes without negative jumps, reflected at the origin. Feedback information about the level of the Lévy process (‘workload level’) may lead to adaptation of the Lévy exponent. Examples of such models are queueing models in which the service speed or customer arrival rate changes depending on the workload level, and dam models in which the release rate depends on the buffer content. We first consider a class of models where information about the workload level is continuously available. In particular, we consider dam processes with a two-step release rule and M/G/1 queues in which the arrival rate, service speed, and/or jump size distribution may be adapted depending on whether the workload is above or below some level K. Secondly, we consider a class of models in which the workload can only be observed at Poisson instants. At these Poisson instants, the Lévy exponent may be adapted based on the amount of work present. For both classes of models, we determine the steady-state workload distribution.

By expressing the discounted net loss process as a randomly weighted sum, we investigate the finite-time ruin probabilities for the Poisson risk model with an exponential Lévy process investment return and heavy-tailed claims. It is found that in finite time, however, the extreme of insurance risk dominates the extreme of financial risk, but, for the case of dangerous investment (see Klüppelberg and Kostadinova (2008) for an accurate definition of dangerous investment), the extreme of financial risk has more and more of an effect on the total risk, and as time passes, the extreme of financial risk finally dominates the extreme of insurance risk.

In the framework of a multitype Bienaymé–Galton–Watson (BGW) process, the event that the daughter's type differs from the mother's type can be viewed as a mutation event. Assuming that mutations are rare, we study a situation where all types except one produce on average less than one offspring. We establish a neat asymptotic structure for the BGW process escaping extinction due to a sequence of mutations toward the supercritical type. Our asymptotic analysis is performed by letting mutation probabilities tend to 0. The limit process, conditional on escaping extinction, is another BGW process with an enriched set of types, allowing us to delineate a stem lineage of particles that leads toward the escape event. The stem lineage can be described by a simple Markov chain on the set of particle types. The total time to escape becomes a sum of a random number of independent, geometrically distributed times spent at intermediate types.

This paper is concerned with a nonstationary Markovian chain of cascading damage that constitutes an iterated version of a classical damage model. The main problem under study is to determine the exact distribution of the total outcome of this process when the cascade of damages finally stops. Two different applications are discussed, namely the final size for a wide class of SIR (susceptible → infective → removed) epidemic models and the total number of failures for a system of components in reliability. The starting point of our analysis is the recent work of Lefèvre (2007) on a first-crossing problem for the cumulated partial sums of independent parametric distributions, possibly nonstationary but stable by convolution. A key mathematical tool is provided by a nonstandard family of remarkable polynomials, called the generalised Abel–Gontcharoff polynomials. Somewhat surprisingly, the approach followed will allow us to relax some model assumptions usually made in epidemic theory and reliability. To close, approximation by a branching process is also investigated to a certain extent.

Suppose that n identical particles evolve according to the same marginal Markov chain. In this setting we study chains such as the Ehrenfest chain that move a prescribed number of randomly chosen particles at each epoch. The product chain constructed by this device inherits its eigenstructure from the marginal chain. There is a further chain derived from the product chain called the composition chain that ignores particle labels and tracks the numbers of particles in the various states. The composition chain in turn inherits its eigenstructure and various properties such as reversibility from the product chain. The equilibrium distribution of the composition chain is multinomial. The current paper proves these facts in the well-known framework of state lumping and identifies the column eigenvectors of the composition chain with the multivariate Krawtchouk polynomials of Griffiths. The advantages of knowing the full spectral decomposition of the composition chain include (a) detailed estimates of the rate of convergence to equilibrium, (b) construction of martingales that allow calculation of the moments of the particle counts, and (c) explicit expressions for mean coalescence times in multi-person random walks. These possibilities are illustrated by applications to Ehrenfest chains, the Hoare and Rahman chain, Kimura's continuous-time chain for DNA evolution, a light bulb chain, and random walks on some specific graphs.

Let Xn(Λ) be the number of nonoverlapping occurrences of a simple pattern Λ in a sequence of independent and identically distributed (i.i.d.) multistate trials. For fixed k, the exact tail probability P{Xn (∧) < k} is difficult to compute and tends to 0 exponentially as n → ∞. In this paper we use the finite Markov chain imbedding technique and standard matrix theory results to obtain an approximation for this tail probability. The result is extended to compound patterns, Markov-dependent multistate trials, and overlapping occurrences of Λ. Numerical comparisons with Poisson and normal approximations are provided. Results indicate that the proposed approximations perform very well and do significantly better than the Poisson and normal approximations in many cases.