Stochastic Geometry and Statistical Applications
The Transparent Dead Leaves Model
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1-20
-
- Article
-
- You have access
- Export citation
Percolation and Connectivity in AB Random Geometric Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 21-41
-
- Article
-
- You have access
- Export citation
Transforming Spatial Point Processes into Poisson Processes Using Random Superposition
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 42-62
-
- Article
-
- You have access
- Export citation
General Applied Probability
An Sir Epidemic Model on a Population with Random Network and Household Structure, and Several Types of Individuals
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 63-86
-
- Article
-
- You have access
- Export citation
Limiting Distributions for a Class Of Diminishing Urn Models
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 87-116
-
- Article
-
- You have access
- Export citation
Pareto Lévy Measures and Multivariate Regular Variation
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 117-138
-
- Article
-
- You have access
- Export citation
Joint Vertex Degrees in the Inhomogeneous Random Graph Model ℊ(n,{pij})
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 139-165
-
- Article
-
- You have access
- Export citation
The Coupon Collector's Problem Revisited: Asymptotics of the Variance
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 166-195
-
- Article
-
- You have access
- Export citation
Numerical Methods for the Exit Time of a Piecewise-Deterministic Markov Process
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 196-225
-
- Article
-
- You have access
- Export citation
Extinction Probability of Interacting Branching Collision Processes
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 226-259
-
- Article
-
- You have access
- Export citation
The Distribution of Foschini's Lower Bound for Channel Capacity
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 260-269
-
- Article
-
- You have access
- Export citation
Asymptotic Conditional Distribution of Exceedance Counts
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 270-291
-
- Article
-
- You have access
- Export citation
Bounds for the Availabilities of Multistate Monotone Systems Based on Decomposition into Stochastically Independent Modules
- Part of:
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 292-308
-
- Article
-
- You have access
- Export citation
Correction
Correction
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. 309-310
-
- Article
-
- You have access
- Export citation
Front Matter
APR volume 44 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Matter
APR volume 44 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

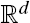 , the
, the 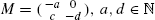 and
and 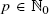 . We determine limiting distributions by obtaining a precise recursive description of the moments of the considered random variables, which allows us to deduce asymptotic expansions of the moments. In particular, we obtain limiting distributions for the pills problem
. We determine limiting distributions by obtaining a precise recursive description of the moments of the considered random variables, which allows us to deduce asymptotic expansions of the moments. In particular, we obtain limiting distributions for the pills problem 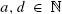 and
and 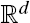 with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called
with Lévy measure Π, emphasizing the dependence between jumps of its components. By transforming the one-dimensional marginal Lévy measures to those of a standard 1-stable Lévy process, we decouple the marginal Lévy measures from the dependence structure. The dependence between the jumps is modeled by a so-called