Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T03:30:29.496Z Has data issue: false hasContentIssue false
  • English
  • Français

Limiting Distributions for a Class Of Diminishing Urn Models

Part of: Combinatorial probability

Published online by Cambridge University Press:  04 January 2016

Markus Kuba  and
Alois Panholzer
Markus Kuba*
Affiliation:
Technische Universität Wien
Alois Panholzer*
Affiliation:
Technische Universität Wien
*
∗ Postal address: Institut für Diskrete Mathematik und Geometrie, Technische Universität Wien Wiedner Hauptstr. 8-10/104, 1040 Wien, Austria.
∗ Postal address: Institut für Diskrete Mathematik und Geometrie, Technische Universität Wien Wiedner Hauptstr. 8-10/104, 1040 Wien, Austria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this work we analyze a class of 2 × 2 Pólya-Eggenberger urn models with ball replacement matrix 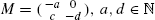and c = pa with 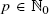. We determine limiting distributions by obtaining a precise recursive description of the moments of the considered random variables, which allows us to deduce asymptotic expansions of the moments. In particular, we obtain limiting distributions for the pills problem a = c = d = 1, originally proposed by Knuth and McCarthy. Furthermore, we also obtain limiting distributions for the well-known sampling without replacement urn, a = d = 1 and c = 0, and generalizations of it to arbitrary 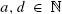and c = 0. Moreover, we obtain a recursive description of the moment sequence for a generalized problem.

Keywords

Pólya-Eggenberger urn modelpills problemsampling without replacementdiminishing urn

MSC classification

Primary: 60C05: Combinatorial probability
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 44 , Issue 1 , March 2012 , pp. 87 - 116
Copyright
© Applied Probability Trust 

Footnotes

This work was supported by the Austrian Science Foundation FWF, grant number S9608-N13.

References

Biane, P., Pitman, J. and Yor, M. (2001). Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions. Bull. Amer. Math. Soc. 38, 435–465.CrossRefGoogle Scholar
Brennan, C. A. C. and Prodinger, H. (2003). The pills problem revisited. Quaest. Math. 26, 427–439.Google Scholar
Crane, E. et al. (2011). The simple harmonic urn. To appear in Ann. Prob.CrossRefGoogle Scholar
Davis, B. (1990). Reinforced random walk. Prob. Theory Relat. Fields 84, 203–229.CrossRefGoogle Scholar
Flajolet, P., Dumas, P. and Puyhaubert, V. (2006). Some exactly solvable models of urn process theory. In Proc. 4th Coll. Math. Comput. Sci. (Discrete Math. Comput. Sci. AG), ed. Chassaing, P., pp. 59–118.Google Scholar
Flajolet, P., Gabarró, J. and Pekari, H. (2005). Analytic urns. Ann. Prob. 33, 1200–1233,CrossRefGoogle Scholar
Graham, R. L., Knuth, D. E. and Patashnik, O. (1994). Concrete Mathematics. Addison-Wesley, Reading, MA.Google Scholar
Greene, D. H. and Knuth, D. E. (1982). Mathematics for the Analysis of Algorithms. Birkhäuser, Boston, MA.Google Scholar
Hwang, H. K., Kuba, M. and Panholzer, A. (2007). Analysis of some exactly solvable diminishing urn models. In Proc. 19th Internat. Conf. Formal Power Series and Algebraic Combinatorics, Nankai University, Tianjin. Available at http://www.fpsac.cn/PDF-Proc./Posters/43.pdf.Google Scholar
Janson, S. (2004). Functional limit theorems for multitype branching processes and generalized Pólya urns. Stoch. Process. Appl. 110, 177–245.CrossRefGoogle Scholar
Janson, S. (2005). Limit theorems for triangular urn schemes. Prob. Theory Relat. Fields 134, 417–452.CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Application. John Wiley, New York.Google Scholar
Kingman, J. F. C. (1999). Martingales in the OK Corral. Bull. London Math. Soc. 31, 601–606.Google Scholar
Kingman, J. F. C. (2002). Stochastic aspects of Lanchester's thoery of warfare. J. Appl. Prob. 39, 455–465,CrossRefGoogle Scholar
Kingman, J. F. C. and Volkov, S. E. (2003). Solution to the OK Corral model via decoupling of Friedman's urn. J. Theoret. Prob. 16, 267–276,Google Scholar
Knuth, D. E. et al. (1992). Problems and solutions: solutions E3429. Amer. Math. Monthly 99, 684.CrossRefGoogle Scholar
Knuth, D. E. and McCarthy, J. (1991). Problem E3429: big pills and little pills. Amer. Math. Monthly 98, 264.Google Scholar
Kotz, S. and Balakrishnan, N. (1997). Advances in urn models during the past two decades. In Advances in Combinatorial Methods and Applications to Probability and Statistics, Birkhäuser, Boston, MA, pp. 203–257.CrossRefGoogle Scholar
Loève, M. (1977). Probability Theory. I, 4th edn. Springer, New York.Google Scholar
Puyhaubert, V. (2005). Modéles d'urnes et phénomènes de seuil en combinatoire analytique. , École Polytechnique.Google Scholar
Stadje, W. (1998). Asymptotic probabilities in a sequential urn scheme related to the matchbox problem. Adv. Appl. Prob. 30, 831–849.Google Scholar
Turner, A. G. (2007). Convergence of Markov processes near saddle fixed points. Ann. Prob. 35, 1141–1171.Google Scholar
Williams, D. and McIlroy, P. (1998). The OK Corral and the power of the law (a curious Poisson-kernel formula for a parabolic equation). Bull. London Math. Soc. 30, 166–170.Google Scholar