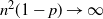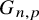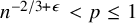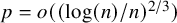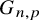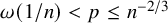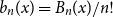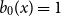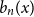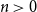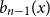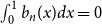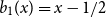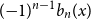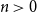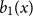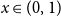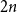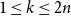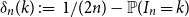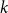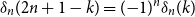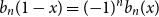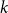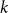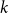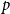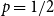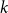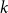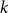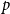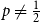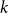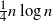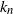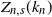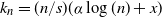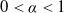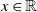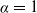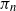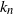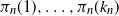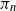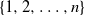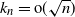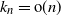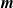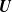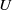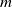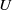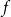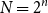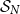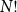292 results in 60Cxx
Depths in random recursive metric spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Central limit theorem for components in meandric systems through high moments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the height process of supercritical Galton–Watson forests with an application to the configuration model in the critical window
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-42
-
- Article
- Export citation
Average Jaccard index of random graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-14
-
- Article
- Export citation
Two-Point Concentration of the Independence Number of the Random Graph
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 February 2024, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 210-237
-
- Article
- Export citation
Anticoncentration in Ramsey graphs and a proof of the Erdős–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 August 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A modification of the random cutting model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 287-314
- Print publication:
- March 2024
-
- Article
- Export citation
Polarised random
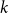 $k$-SAT
$k$-SAT
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 July 2023, pp. 885-899
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Archaeology of random recursive dags and Cooper-Frieze random networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 13 June 2023, pp. 859-873
-
- Article
- Export citation
Unimodular random one-ended planar graphs are sofic
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 09 June 2023, pp. 851-858
-
- Article
- Export citation
Extrema of a multinomial assignment process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 June 2023, pp. 198-213
- Print publication:
- March 2024
-
- Article
- Export citation
Mixing time bounds for edge flipping on regular graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 1317-1332
- Print publication:
- December 2023
-
- Article
- Export citation
Approaching the coupon collector’s problem with group drawings via Stein’s method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1352-1366
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic behaviour of the first positions of uniform parking functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1201-1218
- Print publication:
- December 2023
-
- Article
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic normality for
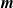 $\boldsymbol{m}$-dependent and constrained
$\boldsymbol{m}$-dependent and constrained 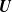 $\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
$\boldsymbol{U}$-statistics, with applications to pattern matching in random strings and permutations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 March 2023, pp. 841-894
- Print publication:
- September 2023
-
- Article
- Export citation
Random feedback shift registers and the limit distribution for largest cycle lengths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 559-593
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random multi-hooking networks
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 13 February 2023, pp. 100-114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Girth, magnitude homology and phase transition of diagonality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 221-247
- Print publication:
- February 2024
-
- Article
- Export citation