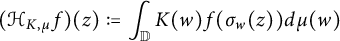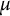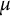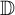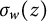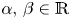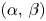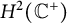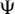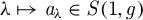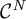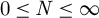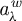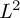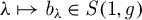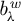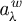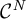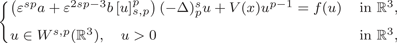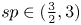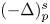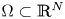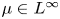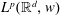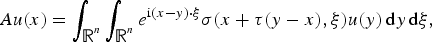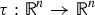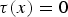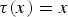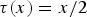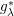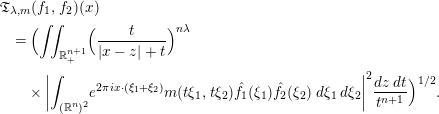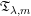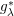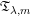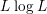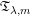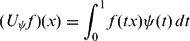34 results in 47Gxx
Propagation of anisotropic Gabor wave front sets
- Part of
- Partial differential equations
- Miscellaneous topics - Partial differential equations
- Integral, integro-differential, and pseudodifferential operators
- Partial differential equations on manifolds; differential operators
- Distributions, generalized functions, distribution spaces
- General quantum mechanics and problems of quantization
- Groups and semigroups of linear operators, their generalizations and applications
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-25
-
- Article
- Export citation
Hausdorff operators on some classical spaces of analytic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-13
-
- Article
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-46
-
- Article
- Export citation
Combined effects in mixed local–nonlocal stationary problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1-47
-
- Article
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Harnack inequality for the nonlocal equations with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1479-1502
- Print publication:
- October 2023
-
- Article
- Export citation
On Hardy kernels as reproducing kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 428-442
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discounted probability of exponential parisian ruin: Diffusion approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 17-37
- Print publication:
- March 2022
-
- Article
- Export citation
Extrapolation to weighted Morrey spaces with variable exponents and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 November 2021, pp. 1002-1027
-
- Article
- Export citation
EQUIVALENCE OF ELLIPTICITY AND THE FREDHOLM PROPERTY IN THE WEYL-HÖRMANDER CALCULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1363-1389
- Print publication:
- July 2022
-
- Article
- Export citation
Concentration of positive solutions for a class of fractional p-Kirchhoff type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 May 2020, pp. 601-651
- Print publication:
- April 2021
-
- Article
- Export citation
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 2682-2718
- Print publication:
- October 2020
-
- Article
- Export citation
Sharp Bounds for Oscillatory Integral Operators with Homogeneous Polynomial Phases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 771-786
- Print publication:
- December 2020
-
- Article
- Export citation
Maximal Operator for the Higher Order Calderón Commutator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 03 September 2019, pp. 1386-1422
- Print publication:
- October 2020
-
- Article
- Export citation
Wave propagation for a class of non-local dispersal non-cooperative systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 14 March 2019, pp. 1965-1997
- Print publication:
- August 2020
-
- Article
- Export citation
Strong maximum principles for fractional elliptic and parabolic problems with mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 475-495
- Print publication:
- February 2020
-
- Article
- Export citation
Pseudo-differential operators with nonlinear quantizing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 103-130
- Print publication:
- February 2020
-
- Article
-
- You have access
- Open access
- Export citation
ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH
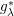 $g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 28 August 2018, pp. 123-152
- Print publication:
- September 2020
-
- Article
- Export citation
FRACTIONAL INTEGRAL OPERATORS ON
 $\unicode[STIX]{x1D6FC}$-MODULATION SPACES IN THE FULL RANGE
$\unicode[STIX]{x1D6FC}$-MODULATION SPACES IN THE FULL RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 499-512
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 28 January 2018, pp. 13-24
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation