Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T02:11:31.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudo-differential operators with nonlinear quantizing functions

Part of: Lie groups Integral, integro-differential, and pseudodifferential operators Abstract harmonic analysis Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  23 January 2019

Massimiliano Esposito  and
Michael Ruzhansky
Massimiliano Esposito
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London, SW7 2AZUnited Kingdom (m.esposito14@imperial.ac.uk; m.ruzhansky@imperial.ac.uk)
Michael Ruzhansky
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, London, SW7 2AZUnited Kingdom (m.esposito14@imperial.ac.uk; m.ruzhansky@imperial.ac.uk)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we develop the calculus of pseudo-differential operators corresponding to the quantizations of the form

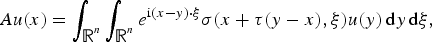$$Au(x)=\int_{{\open R}^n}\int_{{\open R}^n}e^{{\rm i}(x-y)\cdot\xi}\sigma(x+\tau(y-x),\xi)u(y)\,{\rm d}y\,{\rm d}\xi,$$
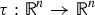where $\tau :{\open R}^n\to {\open R}^n$ is a general function. In particular, for the linear choices 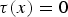$\tau (x)=0$, 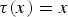$\tau (x)=x$ and 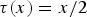$\tau (x)={x}/{2}$ this covers the well-known Kohn–Nirenberg, anti-Kohn–Nirenberg and Weyl quantizations, respectively. Quantizations of such type appear naturally in the analysis on nilpotent Lie groups for polynomial functions τ and here we investigate the corresponding calculus in the model case of 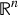${\open R}^n$. We also give examples of nonlinear τ appearing on the polarized and non-polarized Heisenberg groups.

Keywords

Pseudo-differential operatorsquantizationsWeyl quantizationHeisenberg group

MSC classification

Primary: 35S05: Pseudodifferential operators
Secondary: 47G30: Pseudodifferential operators 43A70: Analysis on specific locally compact and other abelian groups 43A80: Analysis on other specific Lie groups 22E25: Nilpotent and solvable Lie groups
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 103 - 130
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © Royal Society of Edinburgh 2019

Footnotes

*

Current address: Department of Mathematics: Analysis, Logic and Discrete Mathematics, Ghent University, Belgium and School of Mathematical Sciences, Queen Mary University of London, United Kingdom.

References

1Bayer, D.. Bilinear time-frequency distributions and pseudodifferential operators. Thesis (Wien: Universität Wien, 2010).Google Scholar
2Calderón, A. and Vaillancourt, R.. On the boundedness of pseudo-differential operators. J. Math. Soc. Japan 23 (1971), 374–378.CrossRefGoogle Scholar
3Cappiello, M. and Toft, J.. Pseudo-differential operators in a Gelfand-Shilov setting. Math. Nachr. 290 (2017), 738–755.CrossRefGoogle Scholar
4Fischer, V. and Ruzhansky, M.. Quantization on nilpotent Lie groups. Progress in Mathematics, Vol. 314 (Birkhäuser, 2016). (open access book).CrossRefGoogle Scholar
5Lerner, N.. Metrics on the phase space and non-selfadjoint pseudo-differetial operators (Birkhäuser, 2010).CrossRefGoogle Scholar
6Mantoiu, M. and Ruzhansky, M.. Pseudo-differential operators, Wigner transform and Weyl systems on type I locally compact groups. Doc. Math. 22 (2017), 1539–1592.Google Scholar
7Ruzhansky, M. and Sugimoto, M.. On global inversion of homogeneous maps. Bull. Math. Sci. 5 (2015), 13–18.CrossRefGoogle Scholar
8Ruzhansky, M. and Sugimoto, M.. Global L 2-boundedness theorems for a class of Fourier integral operators. Comm. Partial Diff. Equ. 31 (2006), 547–569.CrossRefGoogle Scholar
9Ruzhansky, M. and Turunen, V.. Pseudo-differential operators and symmetries (Birkhäuser, 2010).CrossRefGoogle Scholar
10Shubin, M. A.. Pseudodifferential operators and spectral theory (Springer, 2001).CrossRefGoogle Scholar
11Stein, E. M.. Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals (Princeton: Princeton University Press, 1993).Google Scholar
12Taylor, M. E.. Partial differential equations II. Qualitative studies of linear equations, 2nd edn. Applied Mathematical Sciences, 116 (New York: Springer, 2011).Google Scholar
13Toft, J.. Matrix parameterized pseudo-differential calculi on modulation spaces. Generalized functions and Fourier analysis, 215–235, Oper. Theory Adv. Appl., 260, Adv. Partial Differ. Equ. (Basel) (Cham: Birkhäuser/Springer, 2017).CrossRefGoogle Scholar