Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-23T16:59:32.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Concentration of positive solutions for a class of fractional p-Kirchhoff type equations

Part of: Miscellaneous topics - Partial differential equations Integral, integro-differential, and pseudodifferential operators Partial differential equations Classical Topics in Algebraic Topology

Published online by Cambridge University Press:  04 May 2020

Vincenzo Ambrosio Open the ORCID record for Vincenzo Ambrosio [Opens in a new window] ,
Teresa Isernia Open the ORCID record for Teresa Isernia [Opens in a new window]  and
Vicenţiu D. Radulescu
Vincenzo Ambrosio
Affiliation:
Dipartimento di Ingegneria Industriale e Scienze Matematiche, Università Politecnica delle Marche, Via Brecce Bianche, 12, 60131Ancona, Italy (v.ambrosio@univpm.it; t.isernia@univpm.it)
Teresa Isernia
Affiliation:
Dipartimento di Ingegneria Industriale e Scienze Matematiche, Università Politecnica delle Marche, Via Brecce Bianche, 12, 60131Ancona, Italy (v.ambrosio@univpm.it; t.isernia@univpm.it)
Vicenţiu D. Radulescu
Affiliation:
Faculty of Applied Mathematics, AGH University of Science and Technology al. Mickiewicza 30, 30-059 Krakòw (Poland) & Department of Mathematics University of Craiova, 200585Craiova, Romania (radulescu@inf.ucv.ro)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence and concentration of positive solutions for the following class of fractional p-Kirchhoff type problems:

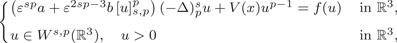$$ \left\{\begin{array}{@{}ll} \left(\varepsilon^{sp}a+\varepsilon^{2sp-3}b \,[u]_{s, p}^{p}\right)(-\Delta)_{p}^{s}u+V(x)u^{p-1}=f(u) & \text{in}\ \mathbb{R}^{3},\\ \noalign{ u\in W^{s, p}(\mathbb{R}^{3}), \quad u>0 & \text{in}\ \mathbb{R}^{3}, \end{array}\right.$$
where ɛ is a small positive parameter, a and b are positive constants, s ∈ (0, 1) and p ∈ (1, ∞) are such that $sp \in (\frac {3}{2}, 3)$, 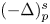$(-\Delta )^{s}_{p}$ is the fractional p-Laplacian operator, f: ℝ → ℝ is a superlinear continuous function with subcritical growth and V: ℝ3 → ℝ is a continuous potential having a local minimum. We also prove a multiplicity result and relate the number of positive solutions with the topology of the set where the potential V attains its minimum values. Finally, we obtain an existence result when f(u) = uq−1 + γur−1, where γ > 0 is sufficiently small, and the powers q and r satisfy 2p < q < p*s ⩽ r. The main results are obtained by using some appropriate variational arguments.

Keywords

Fractional p-Kirchhoff equationvariational methodscritical and supercritical growth

MSC classification

Primary: 47G20: Integro-differential operators
Secondary: 35R11: Fractional partial differential equations 35A15: Variational methods 35B33: Critical exponents 55M30: Ljusternik-Schnirelman (Lyusternik-Shnirel'man) category of a space
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 601 - 651
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alves, C. O., Corrêa, F. J. S. A. and Figueiredo, G. M.. On a class of nonlocal elliptic problems with critical growth. Differ. Equ. Appl. 2 (2010), 409–417.Google Scholar
2Alves, C. O., Corrêa, F. J. S. A. and Ma, T. F.. Positive solutions for a quasilinear elliptic equation of Kirchhoff type. Comput. Math. Appl. 49 (2005), 85–93.CrossRefGoogle Scholar
3Alves, C. O. and Miyagaki, O. H.. Existence and concentration of solution for a class of fractional elliptic equation in ℝN via penalization method. Calc. Var. Partial Differ. Equ. 55 (2016), 47. 19 pp.CrossRefGoogle Scholar
4Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and applications. J. Funct. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
5Ambrosio, V.. Multiplicity of positive solutions for a class of fractional Schrödinger equations via penalization method. Ann. Mat. Pura Appl. (4) 196 (2017), 2043–2062.CrossRefGoogle Scholar
6Ambrosio, V.. An existence result for a fractional Kirchhoff-Schrödinger-Poisson system. Z. Angew. Math. Phys. 69 (2018), 30. 13 pp.CrossRefGoogle Scholar
7Ambrosio, V.. Concentrating solutions for a class of nonlinear fractional Schrödinger equations in ℝN. Rev. Mat. Iberoam. 35 (2019), 1367–1414.CrossRefGoogle Scholar
8Ambrosio, V. and Isernia, T.. A multiplicity result for a fractional Kirchhoff equation in ℝN with a general nonlinearity. Commun. Contemp. Math. 20 (2018), 1750054. 17 pp.CrossRefGoogle Scholar
9Ambrosio, V. and Isernia, T.. Concentration phenomena for a fractional Schrödinger-Kirchhoff type problem. Math. Methods Appl. Sci. 41 (2018), 615–645.Google Scholar
10Ambrosio, V. and Isernia, T.. Multiplicity and concentration results for some nonlinear Schrödinger equations with the fractional p-Laplacian. Discrete Contin. Dyn. Syst. 38 (2018), 5835–5881.CrossRefGoogle Scholar
11Autuori, G., Fiscella, A. and Pucci, P.. Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal. 125 (2015), 699–714.CrossRefGoogle Scholar
12Benci, V. and Cerami, G.. Multiple positive solutions of some elliptic problems via the Morse theory and the domain topology. Calc. Var. Partial Differ. Equ. 2 (1994), 29–48.CrossRefGoogle Scholar
13Bernstein, S.. Sur une classe d'équations fonctionnelles aux dérivées partielles. Bull. Acad. Sci. URSS. Sér. Math. [Izvestia Akad. Nauk SSSR] 4 (1940), 17–26.Google Scholar
14Brézis, H. and Lieb, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
15Caffarelli, L. A. and Silvestre, L.. An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32 (2007), 1245–1260.CrossRefGoogle Scholar
16Chabrowski, J. and Yang, J.. Existence theorems for elliptic equations involving supercritical Sobolev exponent. Adv. Differ. Equ. 2 (1997), 231–256.Google Scholar
17Chipot, M. and Lovat, B.. Some remarks on nonlocal elliptic and parabolic problems. Nonlinear Anal. 30 (1997), 4619–4627.CrossRefGoogle Scholar
18Dávila, J., del Pino, M., Dipierro, S. and Valdinoci, E.. Concentration phenomena for the nonlocal Schrödinger equation with Dirichlet datum. Anal. PDE 8 (2015), 1165–1235.CrossRefGoogle Scholar
19Dávila, J., del Pino, M. and Wei, J.. Concentrating standing waves for the fractional nonlinear Schrödinger equation. J. Differ. Equ. 256 (2014), 858–892.CrossRefGoogle Scholar
20Del Pezzo, L. M. and Quaas, A.. A Hopf's lemma and a strong minimum principle for the fractional p-Laplacian. J. Differ. Equ. 263 (2017), 765–778.CrossRefGoogle Scholar
21Del Pezzo, L. M. and Quaas, A.. Spectrum of the fractional p-Laplacian in ℝN and decay estimate for positive solutions of a Schrödinger equation. Nonlinear Anal. (in press) (2019).CrossRefGoogle Scholar
22Del Pino, M. and Felmer, P. L.. Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4 (1996), 121–137.CrossRefGoogle Scholar
23Di Castro, A., Kuusi, T. and Palatucci, G.. Local behavior of fractional p-minimizers. Ann. Inst. H. Poincaré Anal. Non Linéaire 33 (2016), 1279–1299.CrossRefGoogle Scholar
24Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. math. 136 (2012), 521–573.CrossRefGoogle Scholar
25Dipierro, S., Medina, M. and Valdinoci, E.. Fractional elliptic problems with critical growth in the whole of ℝN. Appunti. Scuola Normale Superiore di Pisa (Nuova Serie) [Lecture Notes. Scuola Normale Superiore di Pisa (New Series)], vol. 15, pp. viii+152 (Pisa: Edizioni della Normale, 2017).CrossRefGoogle Scholar
26Ekeland, I.. On the variational principle. J. Math. Anal. Appl. 47 (1974), 324–353.CrossRefGoogle Scholar
27Felmer, P., Quaas, A. and Tan, J.. Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian. Proc. R. Soc. Edinburgh Sect. A 142 (2012), 1237–1262.CrossRefGoogle Scholar
28Figueiredo, G. M. and Furtado, M.. Positive solutions for some quasilinear equations with critical and supercritical growth. Nonlinear Anal. 66 (2007), 1600–1616.CrossRefGoogle Scholar
29Figueiredo, G. M., Molica Bisci, G. and Servadei, R.. On a fractional Kirchhoff-type equation via Krasnoselskii's genus. Asymptot. Anal. 94 (2015), 347–361.CrossRefGoogle Scholar
30Figueiredo, G. M. and Santos, J. R.. Multiplicity and concentration behavior of positive solutions for a Schrödinger-Kirchhoff type problem via penalization method. ESAIM Control Optim. Calc. Var. 20 (2014), 389–415.CrossRefGoogle Scholar
31Figueiredo, G. M. and Siciliano, G.. A multiplicity result via Ljusternick-Schnirelmann category and Morse theory for a fractional Schrödinger equation in ℝN. NoDEA Nonlinear Differ. Equ. Appl. 23 (2016), 12. 22 pp.CrossRefGoogle Scholar
32Fiscella, A. and Pucci, P.. Kirchhoff-Hardy fractional problems with lack of compactness. Adv. Nonlinear Stud. 17 (2017), 429–456.CrossRefGoogle Scholar
33Fiscella, A. and Valdinoci, E.. A critical Kirchhoff type problem involving a nonlocal operator. Nonlinear Anal. 94 (2014), 156–170.CrossRefGoogle Scholar
34Franzina, G. and Palatucci, G.. Fractional p-eigenvalues. Riv. Math. Univ. Parma (N.S.) 5 (2014), 373–386.Google Scholar
35He, Y., Li, G. and Peng, S.. Concentrating bound states for Kirchhoff type problems in ℝ3 involving critical Sobolev exponents. Adv. Nonlinear Stud. 14 (2014), 483–510.CrossRefGoogle Scholar
36He, X. and Zou, W.. Existence and concentration behavior of positive solutions for a Kirchhoff equation in ℝ3. J. Differ. Equ. 252 (2012), 1813–1834.CrossRefGoogle Scholar
37Iannizzotto, A., Mosconi, S. and Squassina, M.. Global Hölder regularity for the fractional p-Laplacian. Rev. Mat. Iberoam. 32 (2016), 1353–1392.CrossRefGoogle Scholar
38Kirchhoff, G.. Mechanik. (Leipzig: Teubner, 1883).Google Scholar
39Laskin, N.. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268 (2000), 298–305.CrossRefGoogle Scholar
40Liang, S., Molica Bisci, G. and Zhang, B.. Multiple solutions for a noncooperative Kirchhoff-type system involving the fractional p-Laplacian and critical exponents. Math. Nachr. 291 (2018), 1533–1546.CrossRefGoogle Scholar
41Lions, J. L.. On some questions in boundary value problems of mathematical physics, Contemporary developments in continuum mechanics and partial differential equations (Proc. Internat. Sympos., Inst. Mat., Univ. Fed. Rio de Janeiro, Rio de Janeiro, 1977), North-Holland Math. Stud., vol. 30, pp. 284–346 (Amsterdam-New York: North-Holland, 1978).Google Scholar
42Mingqi, X., Molica Bisci, G., Tian, G. and Zhang, B.. Infinitely many solutions for the stationary Kirchhoff problems involving the fractional p-Laplacian. Nonlinearity 29 (2016), 357–374.CrossRefGoogle Scholar
43Mingqi, X., Rădulescu, V. and Zhang, B.. Multiplicity of solutions for a class of quasilinear Kirchhoff system involving the fractional p-Laplacian. Nonlinearity 29 (2016), 3186–3205.CrossRefGoogle Scholar
44Molica Bisci, G., Rădulescu, V. and Servadei, R.. Variational methods for nonlocal fractional problems, with a foreword by Jean Mawhin. Encyclopedia of Mathematics and its Applications, vol. 162 (Cambridge: Cambridge University Press, 2016).CrossRefGoogle Scholar
45Moser, J.. A new proof of De Giorgi's theorem concerning the regularity problem for elliptic differential equations. Commun. Pure Appl. Math. 13 (1960), 457–468.CrossRefGoogle Scholar
46Nyamoradi, N.. Existence of three solutions for Kirchhoff nonlocal operators of elliptic type. Math. Commun. 18 (2013), 489–502.Google Scholar
47Nyamoradi, N. and Zaidan, L. I.. Existence and multiplicity of solutions for fractional p-Laplacian Schrödinger–Kirchhoff type equations. Complex Var. Elliptic Equ. 63 (2018), 346–359.CrossRefGoogle Scholar
48Palatucci, G.. The Dirichlet problem for the p-fractional Laplace equation. Nonlinear Anal. 177 (2018), 699–732.CrossRefGoogle Scholar
49Perera, K. and Zhang, Z.. Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221 (2006), 246–255.CrossRefGoogle Scholar
50Pohožaev, S. I.. A certain class of quasilinear hyperbolic equations. Mat. Sb. 96 (1975), 152–166.Google Scholar
51Pucci, P., Xiang, M. and Zhang, B.. Multiple solutions for nonhomogeneous Schrödinger-Kirchhoff type equations involving the fractional p-Laplacian in ℝN. Calc. Var. Partial Differ. Equ. 54 (2015), 2785–2806.CrossRefGoogle Scholar
52Rabinowitz, P. H.. Variational methods for nonlinear elliptic eigenvalue problems. Indiana Univ. Math. J. 23 (1973/74), 729–754.CrossRefGoogle Scholar
53Rabinowitz, P.. On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
54Simon, J.. Régularité de la solution d'une équation non linéaire dans ℝN. Lectures Notes in Math. No. 665 (Berlin: Springer, 1978).Google Scholar
55Szulkin, A. and Weth, T.. The method of Nehari manifold. In Handbook of nonconvex analysis and applications (eds. D. Y. Gao and D. Montreanu), pp. 597–632 (Boston: International Press, 2010).Google Scholar
56Wang, J., Tian, L., Xu, J. and Zhang, F.. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth. J. Differ. Equ. 253 (2012), 2314–2351.CrossRefGoogle Scholar
57Willem, M., Minimax theorems. Progress in Nonlinear Differential Equations and their Applications, 24. Birkhäuser Boston, Inc., Boston, MA, 1996. x+162 pp.Google Scholar