Article contents
Nonlinear fractional Laplacian problems with nonlocal ‘gradient terms’
Published online by Cambridge University Press: 04 February 2020
Abstract
Let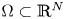 $\Omega \subset \mathbb{R}^{N} $, N ≽ 2, be a smooth bounded domain. For s ∈ (1/2, 1), we consider a problem of the form
$\Omega \subset \mathbb{R}^{N} $, N ≽ 2, be a smooth bounded domain. For s ∈ (1/2, 1), we consider a problem of the form
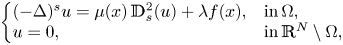 $$\left\{\begin{array}{@{}ll} (-\Delta)^s u = \mu(x)\, \mathbb{D}_s^{2}(u) + \lambda f(x), & {\rm in}\,\Omega, \\ u= 0, & {\rm in}\,\mathbb{R}^{N} \setminus \Omega,\end{array}\right.$$
$$\left\{\begin{array}{@{}ll} (-\Delta)^s u = \mu(x)\, \mathbb{D}_s^{2}(u) + \lambda f(x), & {\rm in}\,\Omega, \\ u= 0, & {\rm in}\,\mathbb{R}^{N} \setminus \Omega,\end{array}\right.$$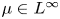 $\mu \in L^{\infty}$ and
$\mu \in L^{\infty}$ and 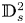 $\mathbb {D}_s^2$ is a nonlocal ‘gradient square’ term given by
$\mathbb {D}_s^2$ is a nonlocal ‘gradient square’ term given by
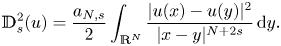 $$\mathbb{D}_s^2 (u) = \frac{a_{N,s}}{2} \int_{\mathbb{R}^{N}} \frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}\,{\rm d}y.$$
$$\mathbb{D}_s^2 (u) = \frac{a_{N,s}}{2} \int_{\mathbb{R}^{N}} \frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}\,{\rm d}y.$$
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2682 - 2718
- Copyright
- Copyright © The Author(s) 2020. Published by The Royal Society of Edinburgh
References
- 6
- Cited by



