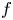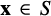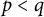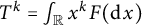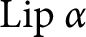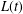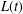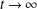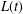66 results in 44Axx
A queue with independent and identically distributed arrivals
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-28
-
- Article
-
- You have access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
The Moment-SOS hierarchy: Applications and related topics
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 841-908
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
QUALITATIVE UNCERTAINTY PRINCIPLE ON CERTAIN LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 289-307
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Two-moment characterization of spectral measures on the real line
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 1369-1392
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A deep look into the dagum family of isotropic covariance functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
- Print publication:
- December 2022
-
- Article
- Export citation
A Laplace transform approach to direct and inverse problems for multi-compartment models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1170-1184
-
- Article
- Export citation
Sampling and interpolation for the discrete Hilbert and Kak–Hilbert transforms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 395-410
- Print publication:
- June 2023
-
- Article
- Export citation
Fourier duality in the Brascamp–Lieb inequality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 387-409
- Print publication:
- September 2022
-
- Article
- Export citation
Estimating tails of independently stopped random walks using concave approximations of hazard functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 773-793
- Print publication:
- September 2021
-
- Article
- Export citation
NONNEGATIVE POLYNOMIALS, SUMS OF SQUARES AND THE MOMENT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 337-341
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation
Renewal in Hawkes processes with self-excitation and inhibition
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 879-915
- Print publication:
- September 2020
-
- Article
- Export citation
Approximation via Hausdorff operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 512-529
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
APPROXIMATION OF AND BY COMPLETELY MONOTONE FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 06 March 2020, pp. 416-430
-
- Article
-
- You have access
- Export citation
Maximal functions associated with families of homogeneous curves: Lp bounds for P ≤ 2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 398-412
-
- Article
- Export citation
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
- Export citation
A support theorem for the X-ray transform on manifolds with plane covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 25 April 2019, pp. 149-158
- Print publication:
- July 2020
-
- Article
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
- Print publication:
- December 2019
-
- Article
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation