Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-09T04:47:38.781Z Has data issue: false hasContentIssue false
  • English
  • Français

LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES

Part of: Stochastic processes Limit theorems Integral transforms, operational calculus

Published online by Cambridge University Press:  16 October 2019

JOSEPH OKELLO OMWONYLEE Open the ORCID record for JOSEPH OKELLO OMWONYLEE [Opens in a new window]
JOSEPH OKELLO OMWONYLEE*
Affiliation:
Department of Mathematics, Makerere University, Kampala, Uganda email jokello@kyu.ac.ug
Get access Rights & Permissions [Opens in a new window]

Abstract

The longest gap 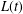$L(t)$ up to time $t$ in a homogeneous Poisson process is the maximal time subinterval between epochs of arrival times up to time $t$; it has applications in the theory of reliability. We study the Laplace transform asymptotics for 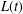$L(t)$ as 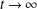$t\rightarrow \infty$ and derive two natural and different large-deviation principles for 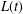$L(t)$ with two distinct rate functions and speeds.

Keywords

longest gapLaplace transformlarge-deviation principlePoisson process

MSC classification

Primary: 60F10: Large deviations
Secondary: 44A10: Laplace transform 60G50: Sums of independent random variables; random walks 60G70: Extreme value theory; extremal processes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 146 - 156
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We acknowledge financial support extended from the Sida bilateral program with Makerere University, phase IV 2015–2020, project 316, Capacity Building in Mathematics and Its Applications.

References

Asmussen, S., Fiorini, P., Lipsky, L., Rolski, T. and Sheahan, R., ‘On the distribution of total task times for tasks that must restart from the beginning if failure occurs’, Math. Oper. Res. 33(4) (2008), 932–944.Google Scholar
Asmussen, S., Ivanovs, J. and Nielsen, A., ‘Time inhomogeneity longest gap and longest run problems’, Stochastic Process. Appl. 127(2) (2017), 574–589.Google Scholar
Chao, M., Fu, J. and Koutras, M., ‘Survey of reliability studies of consecutive-k-out-of-n : F and related systems’, IEEE Trans. Reliab. 44(1) (1995), 120–127.Google Scholar
Deheuvels, P., ‘On the Erdős–Rényi theorem for random fields and sequences and its relationships with the theory of runs and spacings’, Z. Wahrsch. Verw. Gebiete 70(1) (1985), 91–115.Google Scholar
Dembo, A. and Zeitouni, O., Large Deviations Techniques and Applications (Springer, Berlin, 2009).Google Scholar
Devroye, L., ‘Laws of the iterated logarithm for order statistics of uniform spacings’, Ann. Probab. 9(5) (1981), 860–867.Google Scholar
Devroye, L., ‘A log log law for maximal uniform spacings’, Ann. Probab. 10(3) (1982), 863–868.Google Scholar
Erdős, P. and Rényi, A., ‘On a new law of large numbers’, J. Anal. Math. 22 (1970), 103–111.Google Scholar
Erdős, P. and Révész, P., ‘On the length of the longest head run’, Top. Inform. Theory 16 (1975), 219–228.Google Scholar
Fan, R. and Lange, K., ‘Asymptotic properties of the maximal subinterval of a Poisson process’, in: Stochastic Processes, Physics and Geometry: New Interplays. II: A Volume in Honor of Sergio Albeverio, Canadian Mathematical Society Conference Proceedings, 29 (American Mathematical Society, Providence, RI, 2000), 175–187.Google Scholar
Konstantopoulos, T., Liu, Z. and Yang, X., ‘Laplace transform asymptotics and large deviation principles for longest success runs in Bernoulli trails’, J. Appl. Probab. 53 (2016), 747–764.Google Scholar
Liu, Z. and Yang, X., ‘A general large deviation principle for longest runs’, Statist. Probab. Lett. 110 (2016), 128–132.Google Scholar
Omwonylee, J. and Yang, X., ‘Global estimation of distribution function of longest gap’, Preprint, 2019.Google Scholar
Rényi, A., Foundations of Probability (Holden-Day, San Francisco, 1970).Google Scholar