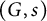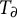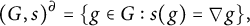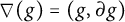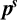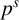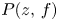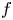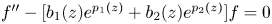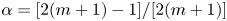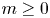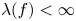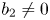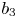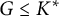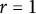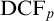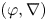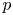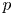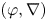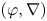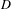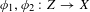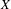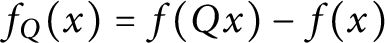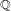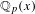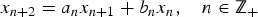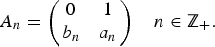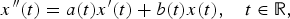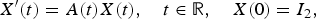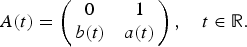41 results in 12Hxx
On definable groups and D-groups in certain fields with a generic derivation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PAC STRUCTURES AS INVARIANTS OF FINITE GROUP ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GHOSTS AND CONGRUENCES FOR
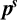 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
- Export citation
Generic differential equations are strongly minimal
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1387-1412
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the oscillation of certain second-order linear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1965-1992
- Print publication:
- December 2023
-
- Article
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting closed asymptotic couples
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 June 2022, pp. 530-555
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY OF DERIVATIONS OF THE FROBENIUS MAP REVISITED
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1213-1229
- Print publication:
- September 2023
-
- Article
- Export citation
Algorithms yield upper bounds in differential algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 29-51
- Print publication:
- February 2023
-
- Article
- Export citation
Logarithmic growth filtrations for
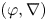 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation
INVARIANT HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 713-739
- Print publication:
- March 2022
-
- Article
- Export citation
Criteria for periodicity and an application to elliptic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 530-540
- Print publication:
- September 2021
-
- Article
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
EQUATIONAL THEORIES OF FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 828-851
- Print publication:
- June 2020
-
- Article
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
Hyers–Ulam stability for equations with differences and differential equations with time-dependent and periodic coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 2175-2188
- Print publication:
- October 2020
-
- Article
- Export citation
AX–SCHANUEL CONDITION IN ARBITRARY CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1157-1213
- Print publication:
- November 2019
-
- Article
- Export citation
Corrigendum: Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2658-2665
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation